服务热线
搜题▪组卷
| x | 1 | 2 | 3 | 4 | 5 |
| y | 7.0 | 6.5 | 5.5 | 3.8 | 2.2 |
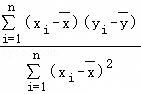 =
=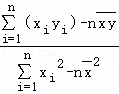 ,
,| 推销员 | A | B | C | D | E |
| 工作年限x(万元) | 2 | 3 | 5 | 7 | 8 |
| 年推销金额y(万元) | 3 | 3.5 | 4 | 6.5 | 8 |
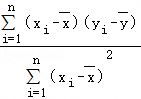 ,
,
| 2月x日 | 11 | 12 | 13 | 14 | 15 |
| 新增病例人数y | 25 | 26 | 29 | 28 | 31 |
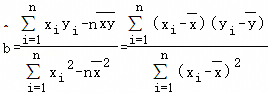 ,
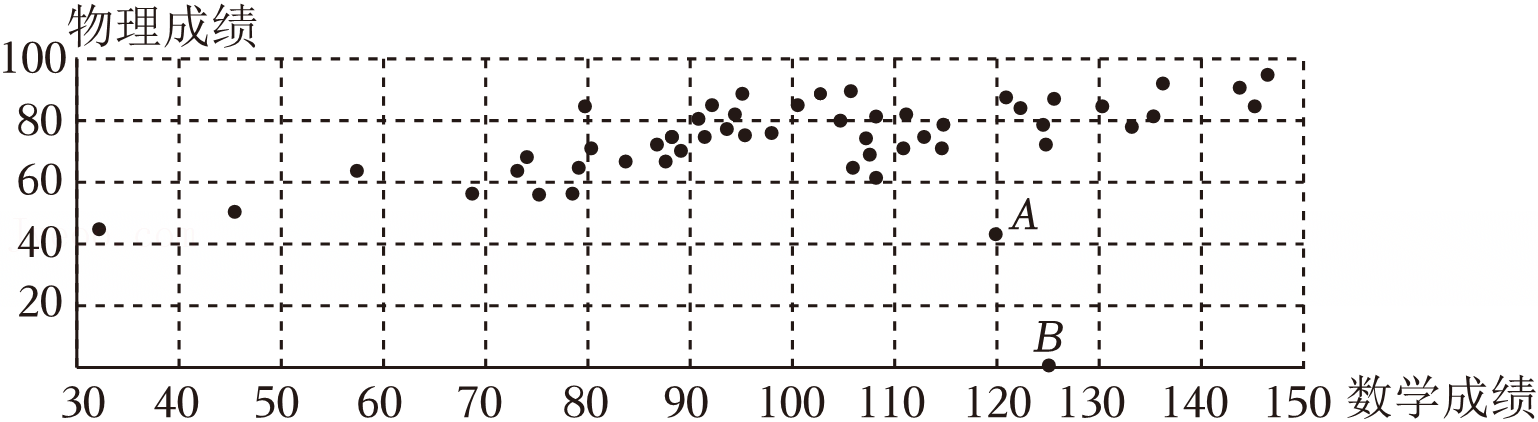
,
| 第n年 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 年收入/亿元 | 23 | 28 | 39 | 43 | 49 | 51 | 53 | 56 | 58 | 60 |
| 商品销售额/万元 | 14 | 18 | 21 | 26 | 29 | 32 | 35 | 38 | 42 | 45 |
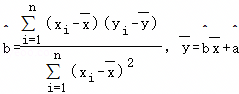 .
.| 学生序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学偏差x | 20 | 15 | 13 | 3 | 2 | ﹣5 | ﹣10 | ﹣18 |
| 物理偏差y | 6.5 | 3.5 | 3.5 | 1.5 | 0.5 | ﹣0.5 | ﹣2.5 | ﹣3.5 |
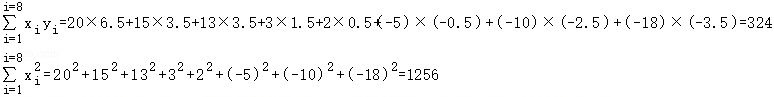 .
.| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售单价xi | 9 | 9.5 | 10 | 10.5 | 11 | 8 |
| 销售量yi | 11 | 10 | 8 | 6 | 5 | 15 |
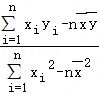 .
.| 日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
| 温差x/℃ | 10 | 11 | 13 | 12 | 8 |
| 发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
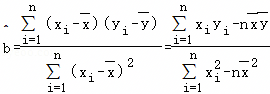 ,
,| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
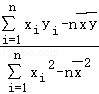 =
=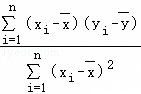 ,
,| 周光照量X(单位:小时) | 30<X<50 | 50≤X≤70 | X>70 |
| 光照控制仪最多可运行台数 | 3 | 2 | 1 |
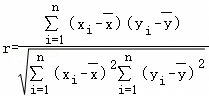 ,参考数据
,参考数据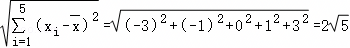
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
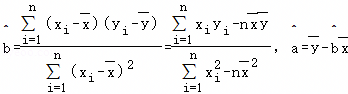 ,
,| x | 1 | 2 | 3 | 4 | 5 |
| y | 70 | 65 | 55 | 38 | 22 |
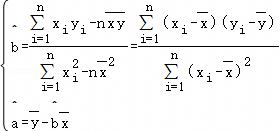 .)
.)| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 小明成功次数 | 16 | 20 | 20 | 25 | 30 | 36 | a |
| 小红成功次数 | 16 | 22 | 25 | 26 | 32 | 35 | 35 |
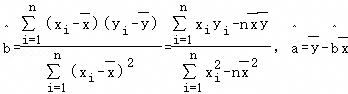 .
.| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
| 根部横截面积xi | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
| 材积量yi | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
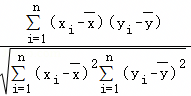 ,
,| 样本号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 总和 |
| 根部横截面积xi | 0.04 | 0.06 | 0.04 | 0.08 | 0.08 | 0.05 | 0.05 | 0.07 | 0.07 | 0.06 | 0.6 |
| 材积量yi | 0.25 | 0.40 | 0.22 | 0.54 | 0.51 | 0.34 | 0.36 | 0.46 | 0.42 | 0.40 | 3.9 |
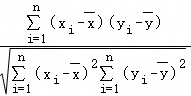 ,
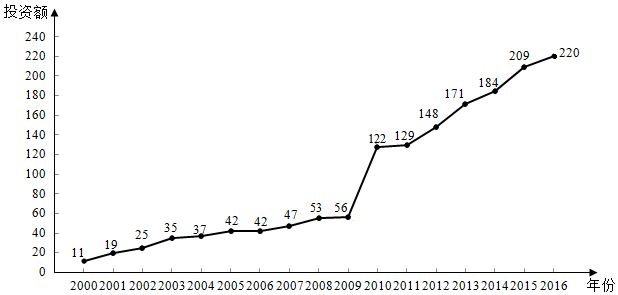
,

dygzsxyn
2020-05-21
高中数学 | 高二下 | 解答题