服务热线
搜题▪组卷
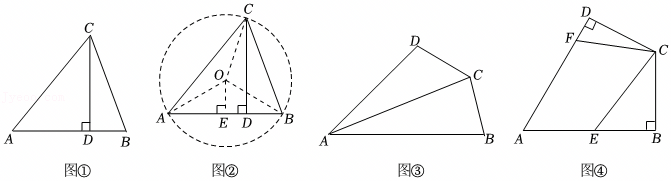
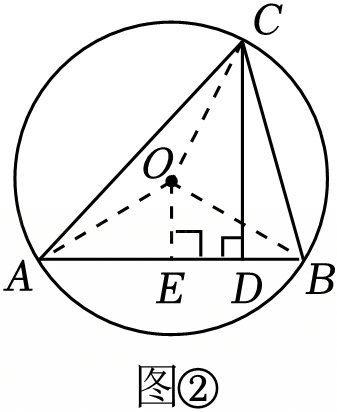
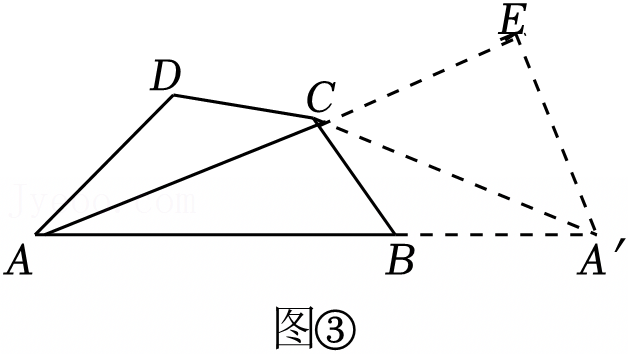
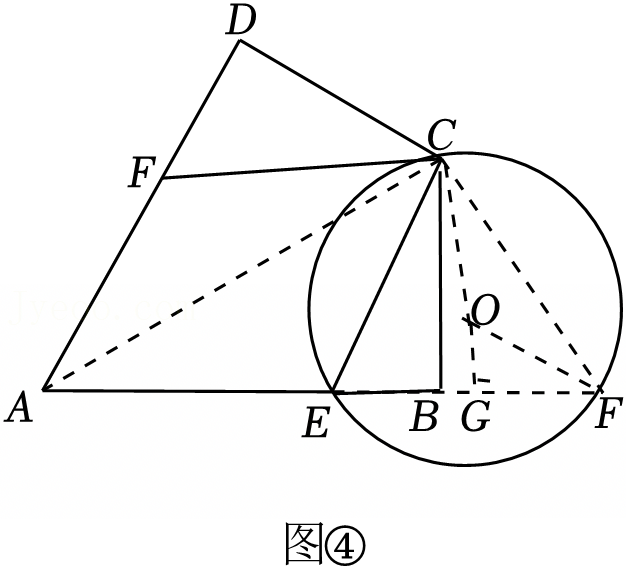
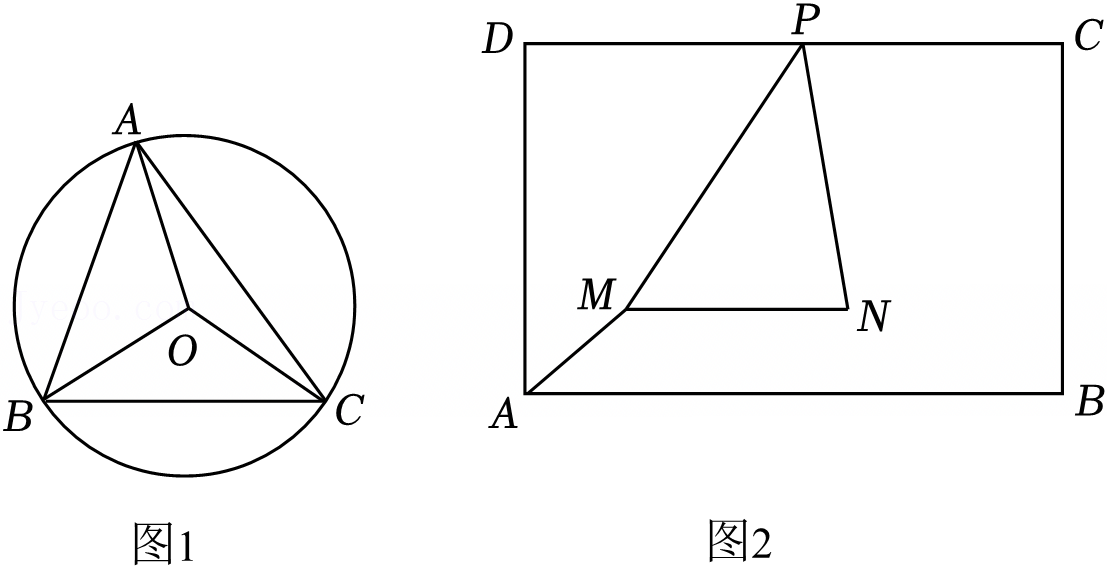
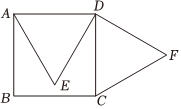 综合与实践
综合与实践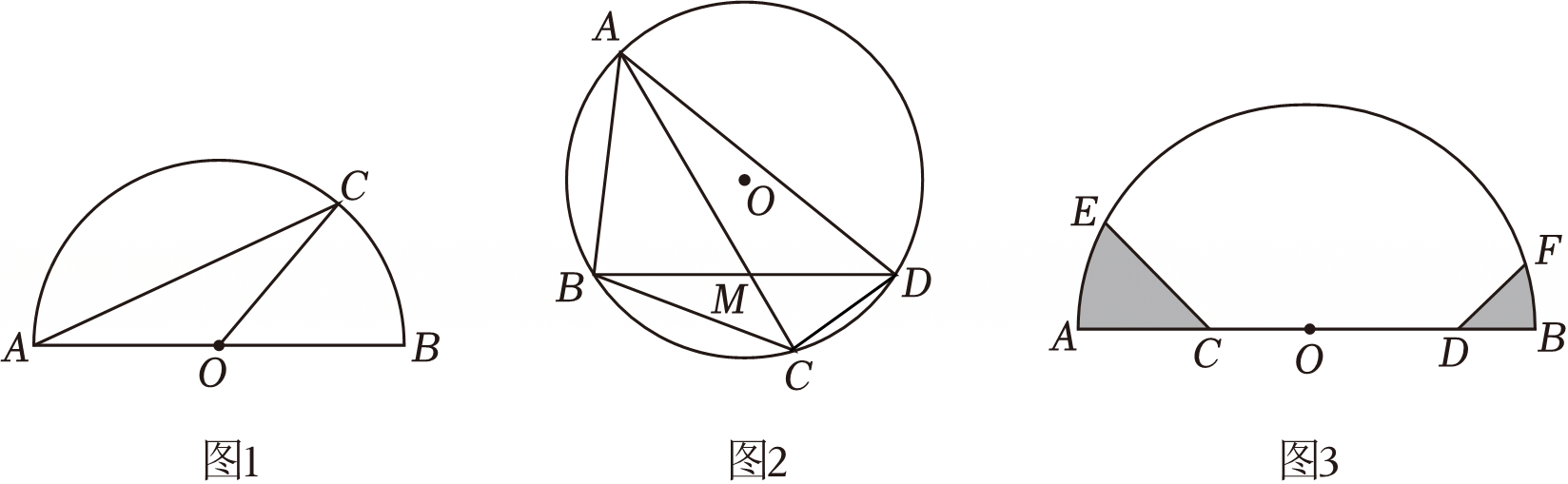
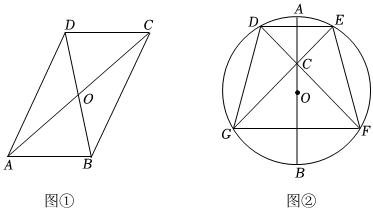
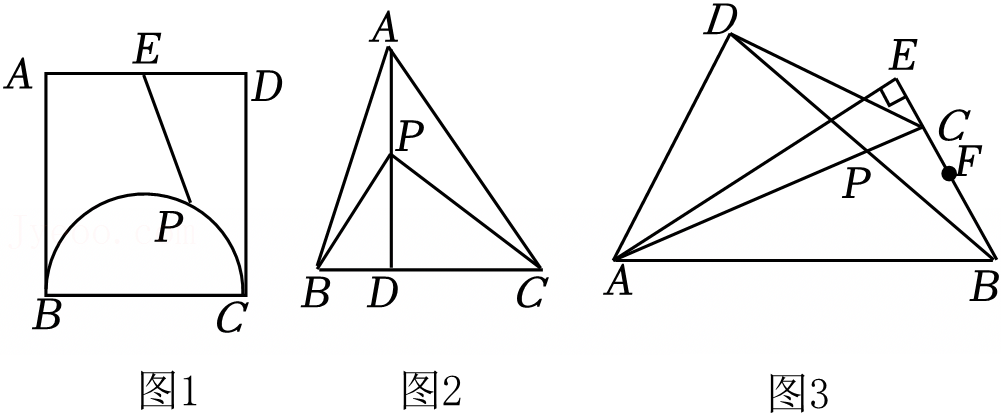
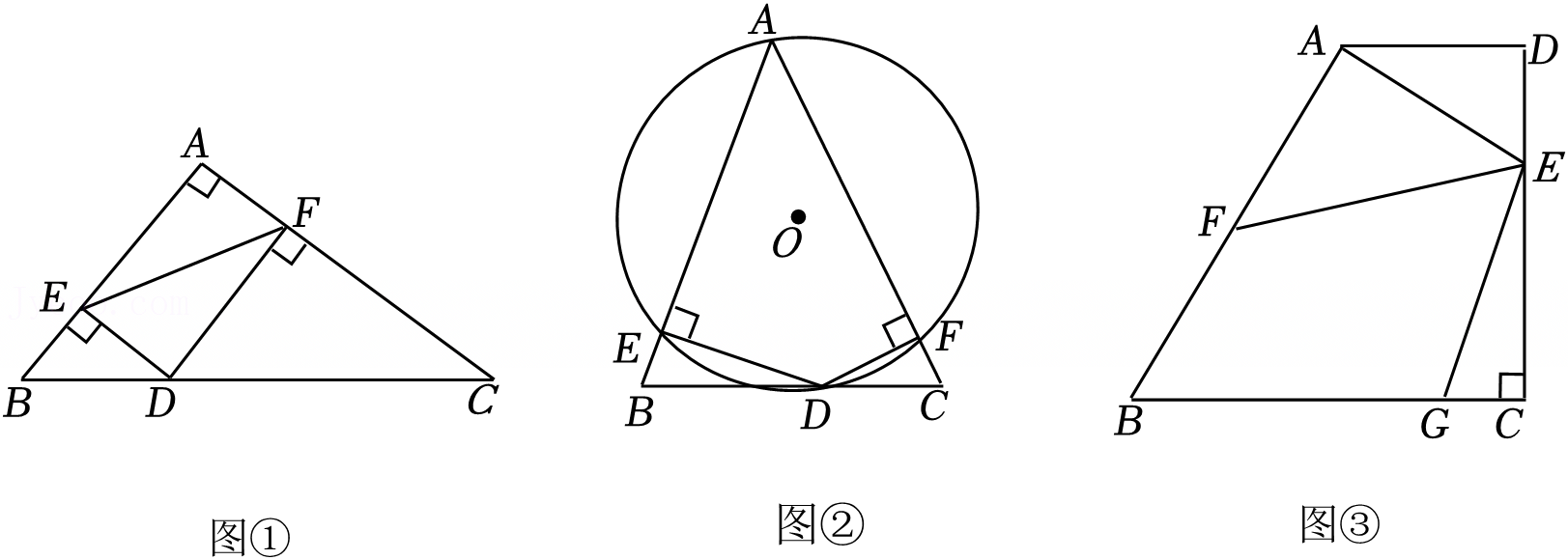
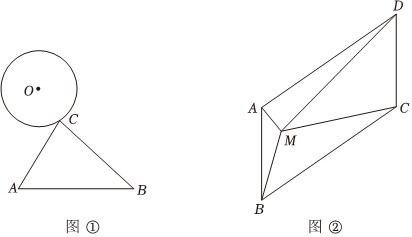
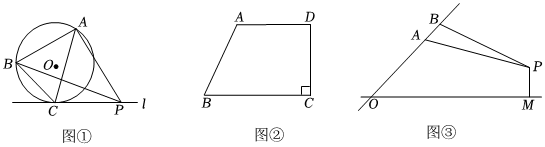

zcf@dyw.com
2025-04-02
初中数学 | | 解答题