已知乒乓球桌的长度为某人从球桌边缘正上方高处将乒乓球向正前方抛向对面桌面乒乓球的运动路线近似是抛物线的一部分建立如图所示的平面直角坐标系从乒乓球抛出到第一次落在球桌的过程中乒乓球的竖直高度单位与水平距离单位近似满足函数关系乒乓球的水平距离与竖直高度的几组数据如表所示根据表中数据直接写出乒乓球竖直高度的最大值并求出满足的函数关系式水平距离竖直高度

首页 > 试题列表 > 单题解析

211618. （2025•高新一中•三模）已知乒乓球桌的长度为274cm,某人从球桌边缘正上方高18cm处将乒乓球向正前方抛向对面桌面，乒乓球的运动路线近似是抛物线的一部分．
（1）建立如图2所示的平面直角坐标系，从乒乓球抛出到第一次落在球桌的过程中，乒乓球的竖直高度y（单位：cm）与水平距离x（单位：cm）近似满足函数关系y=a（x-h₁）²+k（a＜0）．
$德优题库$
乒乓球的水平距离x与竖直高度y的几组数据如表所示．根据表中数据，直接写出乒乓球竖直高度的最大值，并求出满足的函数关系式；

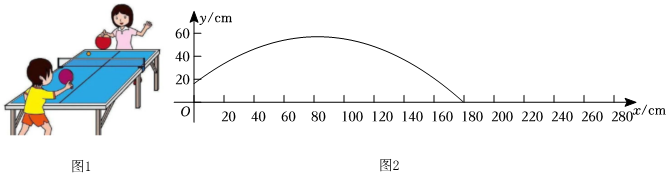
水平距离x/cm	0	40	80	120	160
竖直高度y/cm	18	42	50	42	18

（2）乒乓球第一次落在球桌后弹起，它的竖直高度y与水平距离x近似满足函数关系y=-0.005（x-h₂）²+8．判断乒乓球再次落下时是否仍落在球桌上，并说明理由．

共享时间:2025-04-04 难度:1

纠错

下载

相似

组卷白板

[考点]

二次函数的应用题，

[答案]

（1）乒乓球竖直高度的最大值为50cm，y与x的函数关系式为y＝﹣0.05（x﹣80）²+50；

（2）乒乓球再次落下时仍落在球桌上．

[解析]

解：（1）由表中数据可知，乒乓球竖直高度的最大值为50cm，h₁＝80，k＝50；
∴y与x的函数关系式为y＝a（x﹣80）²+50，
把（0，18）代入函数解析式得：18＝a×80²+50，
解得a＝﹣0.005，
∴y与x的函数关系式为y＝﹣0.005（x﹣80）²+50；
（2）令y＝0，则﹣0.005（x﹣80）²+50＝0，
解得x＝180或x＝﹣20（舍去），
∴球第一次落在球桌面上的点为（180，0），
把（180，0）代入y＝﹣0.005（x﹣h₂）²+8得：
﹣0.005（180﹣h₂）²+8＝0，
解得h₂＝140（舍去）或h₂＝220，
∴乒乓球第一次落在球桌后弹起，它的竖直高度y与水平距离x近似满足函数关系y＝﹣0.005（x﹣220）²+8，
当y＝0时，0＝﹣0.005（x﹣220）²+8，
解得x＝260或x＝180（舍去），
∵260＜274，
∴乒乓球再次落下时仍落在球桌上．

[点评]

本题考查了"二次函数的应用题，"，属于"基础题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

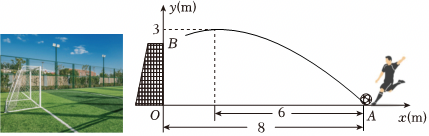
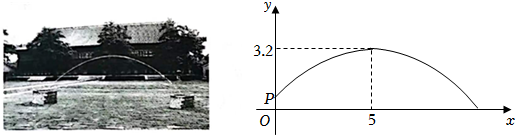
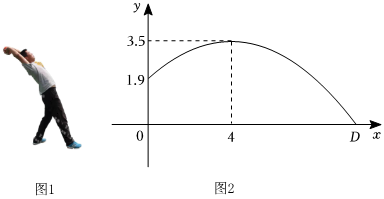
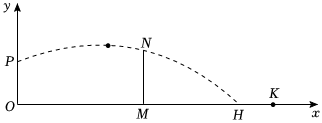190493. （2025•碑林区•九上期末） $德优题库$ 排球运动是一种全身性的体育活动，它能够有效提升心肺功能，改善柔韧性和协调性．一名排球运动员在原点O处训练发球，球网MN高2.4m,与原点O的水平距离OM为9m,且MN与地面垂直，球场的边界（点K）与原点O的水平距离为18m,排球（看作点）从点O的正上方点P（0，2）处发出，排球经过的路径可以看作抛物线的一部分，当排球在距离发出点水平距离6m时，与地面的垂直距离最大，为3m,落地点为点H，如图，以点O为原点，点O，M，H，K所在的直线为x轴，OP所在直线为y轴，建立平面直角坐标系．（图中所有的点均在同一平面内）．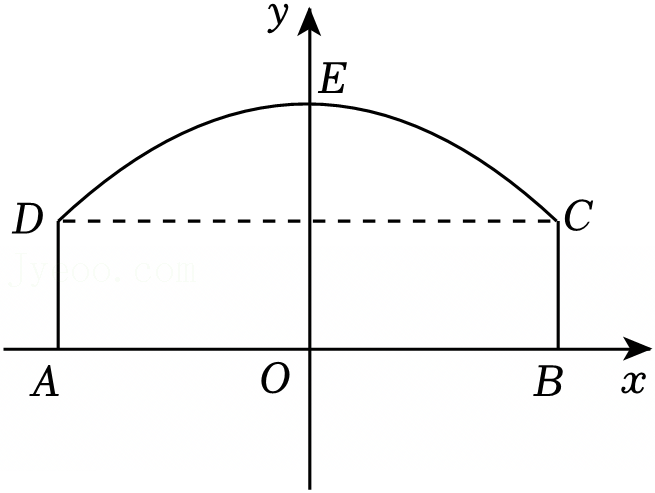
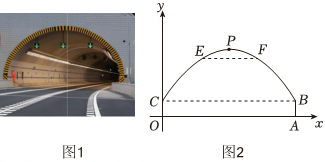
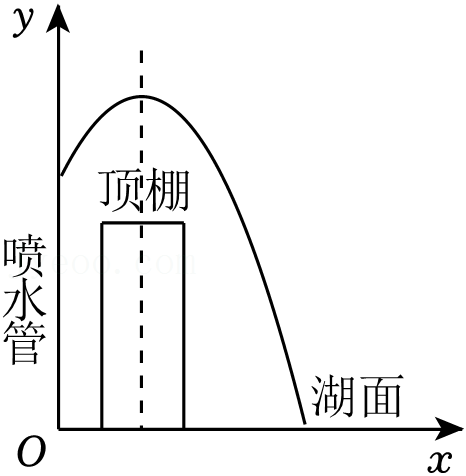
（1）求排球经过路径所在抛物线的函数表达式．
（2）通过计算判断发出后的排球能否越过球网？是否会出界？

共享时间:2025-02-05 难度:1 相似度:2

解析

纠错

下载

组卷白板

174149. （2024•铁一中学•九上二月）如图，隧道的截面由抛物线和长方形构成．长方形的长为16m，宽为4m，抛物线的最高点E离路面AB的距离为8m．
（1）按如图所示的直角坐标系，求表示该抛物线的函数表达式；
（2）一大型货运汽车装载某大型设备后高为7m，宽为4m．若该隧道内设单向行车道，那么这辆货车能否安全通过？请说明理由．

共享时间:2024-12-28 难度:1 相似度:2

解析

纠错

下载

组卷白板

173819. （2024•高新一中•九上三月）一次足球训练中，小明从球门正前方8m的A处射门，球射向球门的路线呈抛物线．当球飞行的水平距离为6m时，球达到最高点，此时球离地面3m．已知球门高OB为2.44m，现以O为原点建立如图所示直角坐标系．
（1）求抛物线的函数表达式，并通过计算判断球能否射进球门（忽略其他因素）；
（2）对本次训练进行分析，若射门路线的形状、最大高度均保持不变，则当时他应该带球向正后方移动多少米射门，才能让足球经过点O正上方2.25m处？

共享时间:2024-01-25 难度:1 相似度:2

解析

纠错

下载

组卷白板

174978. （2024•西安三中•九上二月）打水漂是小伙伴们经常玩的游戏，如图，水漂从水面上（点O）第一次飞起，飞行的最大高度为0.5米，第二次从距离O点4米的A处飞起．据试验，水漂在水面弹起的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半：
（1）求水漂第二次飞越时，该抛物线的函数表达式；
（2）若此次水漂可以在水面上飞越2次，且第一次击打水面时距离河岸1米，问水漂能否飞过8米宽的河面．

共享时间:2024-12-29 难度:1 相似度:2

解析

纠错

下载

组卷白板

173212. （2024•西光中学•九上二月）国庆期间某旅游点一家商铺销售一批成本为每件50元的商品，规定销售单价不低于成本价，又不高于每件70元，销售量y（件）与销售单价x（元）的关系可以近似的看作一次函数（如图）．
（1）请直接写出y关于x的函数表达式　y＝﹣10x+1000　；
（2）设该商铺销售这批商品获得的总利润为w元，当销售单价为多少元时，可获得的总利润最大？最大总利润是多少？

共享时间:2024-12-10 难度:1 相似度:2

解析

纠错

下载

组卷白板

173031. （2024•高新一中•九上二月）小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m,水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为y=a（x-h）²+k,其中x（m）是水柱距喷水头的水平距离，y（m）是水柱距地面的高度．
（1）求抛物线的表达式．
（2）爸爸站在水柱正下方，且距喷水头P水平距离3m.身高1.6m的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离．
$德优题库$

共享时间:2024-12-16 难度:1 相似度:2

解析

纠错

下载

组卷白板

172962. （2024•高新一中•九上二月）某种蔬菜的销售单价与销售月份之间的关系如图1所示，成本与销售月份之间的关系如图2所示（图1的图象是线段，图2的图象是抛物线），已知市场部销售该种蔬菜4、5两个月的总收益为220000元，且5月份的销售量比4月份的销售量多20000千克，求4、5两个月的销售总量．

共享时间:2024-12-21 难度:1 相似度:2

解析

纠错

下载

组卷白板

175952. （2024•交大附中•九上二月）如图，一个横断面为抛物线形的拱桥，当水面宽6m时，拱顶离水面3m.以桥孔的最高点为原点，过原点的水平线为x轴，建立平面直角坐标系．当水面下降1m时，求此时水面的宽度是多少米？
$德优题库$

共享时间:2024-12-24 难度:1 相似度:2

解析

纠错

下载

组卷白板

172867. （2024•逸翠园中学•九上四月）小李在景区销售一种旅游纪念品，已知每件进价为6元，当销售单价定为8元时，每天可以销售200件，市场调查反映：销售单价每提高1元，日销量将会减少10件，物价部门规定：销售单价不能超过12元，设该纪念品的销售单价为x（元），日销量为y（件），日销售利润为w（元）．
（1）求y与x的函数关系式；
（2）求日销售利润w（元）与销售单价x（元）的函数关系式，当x为何值时，日销售利润最大，并求出最大利润．

共享时间:2024-01-28 难度:1 相似度:2

解析

纠错

下载

组卷白板

172515. （2024•师大附中•九上二月）高速隧道是为了更好地适应地形、保护环境、节省土地和提高通行效率等方面的需要，除此之外高速隧道还有重要的战略意义．如图所示，某高速隧道的下部近似为矩形OABC，上部近似为一条抛物线．已知OA＝10米，AB＝1米，高速隧道的最高点P（抛物线的顶点）离地面OA的距离为6米．
（1）建立如图所示的平面直角坐标系，求抛物线的解析式；
（2）若在高速隧道入口的上部安装两个车道指示灯E，F，若平行线段EF与BC之间的距离为

米，则点E与隧道左壁OC之间的距离为多少米？

共享时间:2024-12-22 难度:1 相似度:2

解析

纠错

下载

组卷白板

61342. （2023•爱知中学•九上期末）掷实心球是中考体育考试项目之一，如图1是一名男生投实心球情境，实心球行进路线是一条抛物线，行进高度y（m）与水平距㐫x（m）之间的函数关系如图2所示．掷出时，起点处高度为1.9m,当水平距离为4m时，实心球行进至最高点3.5m处．
$德优题库$
（1）求y关于x的函数表达式；
（2）根据陕西中考体育考试评分标准（男生版），投掷过程中，实心球从起点到落地点的水平距离大于等于9.6m时，即可得该项目满分100分．该男生在此项考试中能否得满分，请说明理由．

共享时间:2023-03-02 难度:1 相似度:2

解析

纠错

下载

组卷白板

27857. （2023•爱知中学•九上期末）有一种工艺品很受大家喜欢，某工厂原来有6条生产线，为了加快生产，工厂准备改造生产线，如果增加x条生产线后，每条生产线可以生产y个工艺品，经过市场调查发现：y与x满足的关系式为y=-10x+100．如果设该厂每天可以生产的工艺品w个．
（1）请写出w与x的函数关系式；
（2）请求出该工厂增加多少条生产线时，每天生产的工艺品的数量最多，最多为多少个？

共享时间:2024-01-30 难度:1 相似度:2

解析

纠错

下载

组卷白板

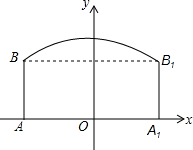27754. （2023•航天中学•九上二月） $德优题库$ 如图，隧道的截面由抛物线和长方形构成，长方形的长为16m,宽为6m,抛物线的最高点C离地面AA₁的距离为8m.
（1）按如图所示的直角坐标系，求表示该抛物线的函数表达式．
（2）一大型汽车装载某大型设备后，高为7m,宽为4m,如果该隧道内设双向行车道，那么这辆货车能否安全通过？

共享时间:2023-10-10 难度:1 相似度:2

解析

纠错

下载

组卷白板

25782. （2024•高新一中•五模）某校课外科技活动兴趣小组研制了一种航模飞机，这种航模飞机飞行的轨迹可以看作是抛物线的一部分．活动小组在水平安全线上设置一个高度可以变化的发射平台，当发射平台的高度变化时，飞机飞行的轨迹可视为抛物线上下平移得到．如图所示，以水平安全线上发射平台所在位置A为坐标原点，以水平安全线为x轴，建立平面直角坐标系．
通过实验，在A处发射飞机，收集到飞机相对于出发点的飞行水平距离x（单位：m）与飞行高度y（单位：m）的部分对应数值如表．

飞行水平距离x/m	0	20	30	50	80	…
飞行高度y/m	0	40	54	70	64	…

根据上面的信息，解决下列问题：
（1）当活动小组在A处发射飞机时，求飞机落到水平安全线时飞行水平距离；
（2）在水平安全线上设置回收区域MN，AM=125m,MN=5m,若飞机能落到回收区域MN内（不包括端点M，N），求发射平台相对于安全线的高度的变化范围．
$德优题库$

共享时间:2024-04-20 难度:4 相似度:2

解析

纠错

下载

组卷白板

181107. （2024•爱知中学•九下一月）某公园的人工湖里安装一个喷泉，在湖中心竖直安装了一根高为3米的喷水管，它喷出的抛物线形水柱在与喷水管的水平距离为1米处达到最高，水柱落地处离喷水管3米．以喷水管与湖面的交点为原点，建立如图的平面直角坐标系．
（1）求抛物线的函数表达式；
（2）现公园准备通过只调节喷头露出湖面的高度，使得游船能从抛物线水柱下方正中间通过．为避免游客被喷泉淋湿，要求游船从抛物线水柱下方正中间通过时，游船顶棚上任意一点到水柱的竖直距离均不小于1.5米，已知游船顶棚宽度为1米，顶棚到湖面的高度为2.5米，那么公园应将喷头至少向上移动多少米才能符合要求？

共享时间:2024-04-24 难度:1 相似度:2

解析

纠错

下载

组卷白板

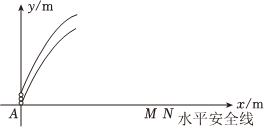
xt@dyw.com

2025-04-04

初中数学 | | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2025年陕西省西安市高新一中中考数学三模试卷

更新:2025-04-04 09:58浏览量:39

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手