服务热线
搜题▪组卷
| 活动目的 | 测量某雕塑的高度 | |
| 活动方案 | 方案一 | 方案二 |
| 示意图 |  |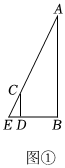
 |
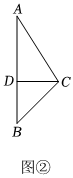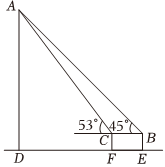
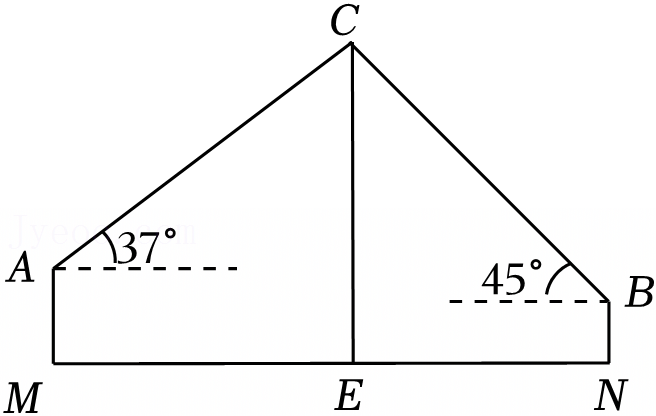
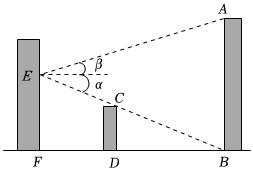
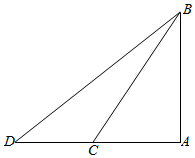
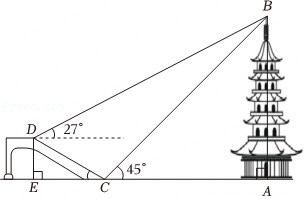
| 说明 | 如图①，在天气晴朗的一天，阳阳站在水平地面上的点D处，他的影子顶端恰好与该雕塑AB的影子顶端E重合，小组成员用皮尺测出阳阳的身高CD、影长DE，以及阳阳到雕塑AB的距离BD．图中所有的点都在同一平面内，点B、D、E在同一水平线上，且AB⊥BE，CD⊥BE． | 如图②，小组成员用无人机在点C处测得该雕塑的顶端A处的仰角为∠ACD，雕塑的底端B处的俯角为∠DCB，无人机距离雕塑的水平距离为CD，雕塑AB垂直于地面，AB⊥CD，A、B、C、D在同一平面内． |
| 测量数据 | CD=1.8m,DE=0.6m,BD=4.6m | ∠ACD=58°，∠DCB=45°，CD=6m |
，
＝
，
| 课题 | 测量人工湖岸边一棵树的高度 | |
| 成员 | 组长：瑛瑛 组员：小明、小华、小晴 |
|
| 测量工具 | 测角仪、皮尺 | |
| 测量示意图及测量数据 |  |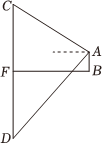
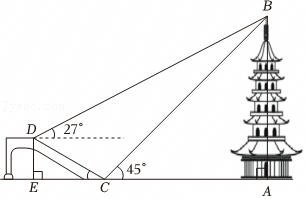
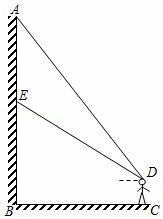
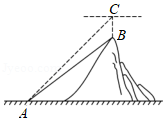
说明：线段CF表示所要测量树的高度．测量者在岸边点B处清晰地看到这棵树倒映在平静的湖面上，并测得该树顶端C的仰角为30°，树的顶端C在水中的倒影D的俯角为45°．测量者的眼睛距湖面的高度AB=1.6m,点B，F在同一水平直线上，AB⊥BF，CF⊥BF，点A，B，C，D，F在同一平面内. |
| 实施说明 | 测量树的顶端在水中倒影的俯角，测得的角度有一点误差，结果的误差就会很大，经多次测量取其平均值．（光线的折射忽略不计） | |
=1.73，
≈1.41）
，cos53°≈
，tan53°≈
）
，
，
）
，点E，C，A在同一条水平直线上．某学习小组在观景台C处测得塔顶部B的仰角为45°，在观景台D处测得塔顶部B的仰角为27°．
≈1.7）
≈1.73，sin48°≈0.74，cos48°≈0.67，tan48°≈1.11，sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）
≈1.7，
≈1.4，结果保留一位小数） 
，点E，C，A在同一条水平直线上．某学习小组在观景台C处测得塔顶部B的仰角为45°，在观景台D处测得塔顶部B的仰角为27°，求塔AB的高度．（结果精确到个位）
≈1.7）
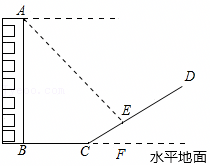
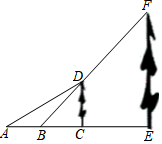
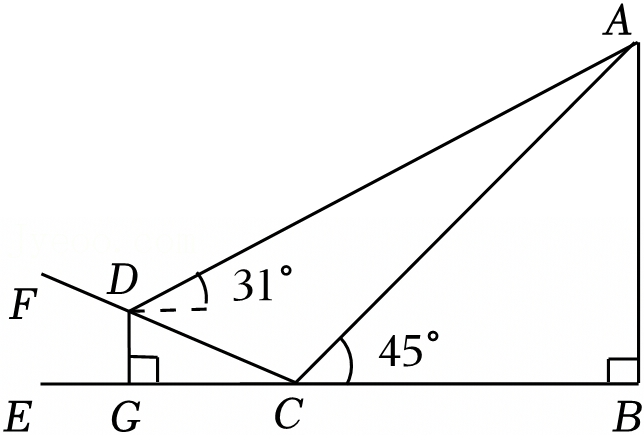
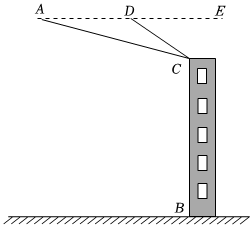无人机在实际生活中的应用广泛，如图所示，某人利用无人机测大楼的高度BC，无人机在空中点A处，测得点A与地面距离80米，测得C点的俯角∠EAC=14°，控制无人机水平移动至点D，测得AD=21米，楼顶C点的俯角∠EDC=31°，点A、B、C、D在同一平面内，求大楼的高度BC．（sin14°≈0.24，cos14°≈0.97，tan14°≈0.25；sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）
xt@dyw.com
2025-03-04
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
