服务热线
搜题▪组卷
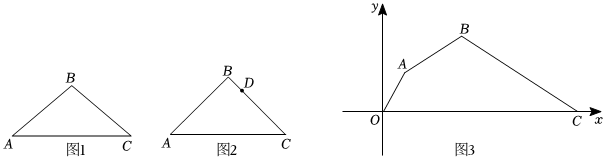
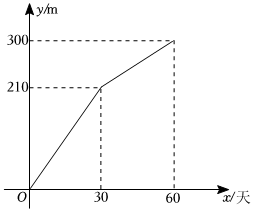 甲、乙两个工程组同时挖掘某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
甲、乙两个工程组同时挖掘某段隧道,两组每天挖掘长度均保持不变,合作一段时间后,乙组因维修设备而停工,甲组单独完成了剩下的任务,甲、乙两组挖掘的长度之和y(m)与甲组挖掘时间x(天)之间的关系如图所示.
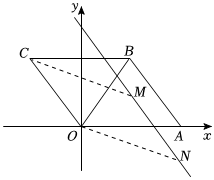 如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A,C两点的坐标分别为(6,0),(-3,4).将线段CO先向右平移6个单位后,再向下平移2个单位,得到线段MN.
如图,在平面直角坐标系xOy中,四边形OABC是平行四边形,A,C两点的坐标分别为(6,0),(-3,4).将线段CO先向右平移6个单位后,再向下平移2个单位,得到线段MN.


dyczsxyn
2025-06-03
初中数学 | | 解答题