服务热线
搜题▪组卷
米，∠ADE＝150°，∠BCE＝135°．
，∠EDK＝∠ADE﹣∠ADC＝60°，
，
，
，
（m2），
，
，即
，
，
，
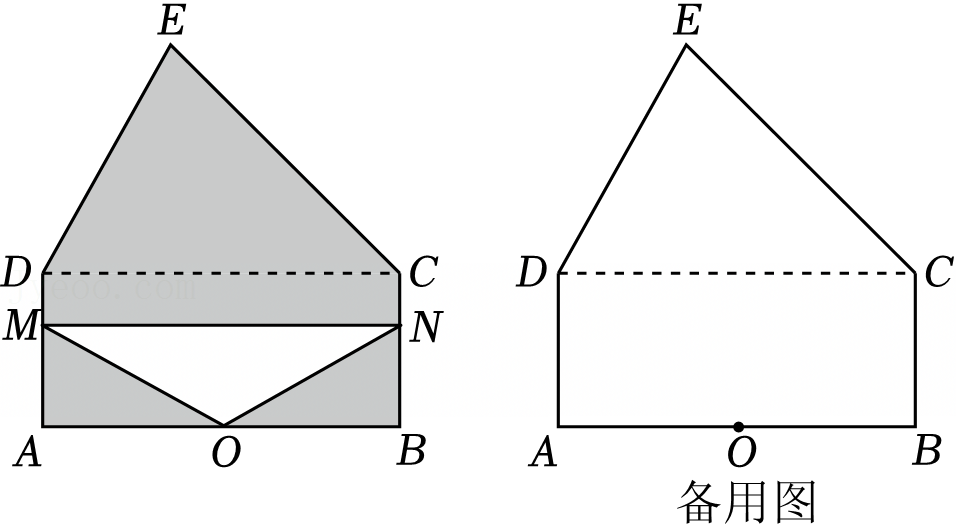
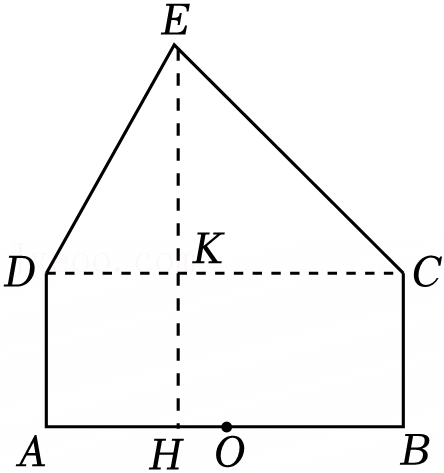
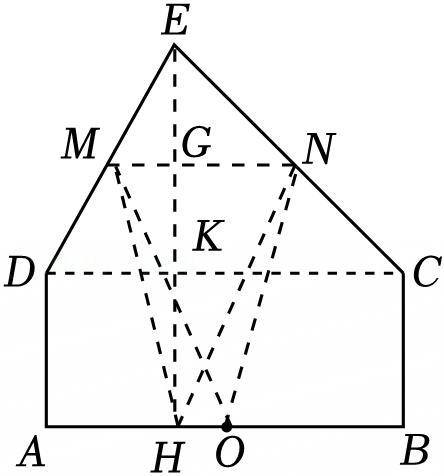
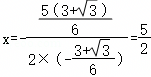时，y有最大值为
，
，
．
米，∠ABC＝∠DCB＝135°，现对该区域景观进行改造提升，在距离B点250米的点E处作EF⊥AB，使得EF＝180米，在EF上确定点G，使得FG＝120米，计划在FG段建造水幕电影，计划在BE上找一点M，在CD上找一点N，将四边形MBCN设计为儿童嬉水区，在湖中的点O处拟建造一个观影平台，使得O到M，N的距离相等，且∠MON＝90°，在△MON区域种植荷花等水生花卉．
．其中，当火箭运行的水平距离为9km时，自动引发火箭的第二级．若火箭第二级的引发点的高度为3.6km．
大雁塔是西安市的标志性建筑和著名古迹，是古城西安的象征．因此西安市徽中央所绘制的便是这座著名古塔．我校社会实践小组为了测量大雁塔的高度AB，在地面上立两根高为2m的标杆CD和GH，两杆之间的距离CG=62米，点G、C、B成一线．从C处退行4米到点E处，人的眼睛贴着地面观察A点，A、D、E三点成一线；从G处退行6米到点F处，从F观察A点，A、F、H也成一线．请你根据以上数据，计算大雁塔的高度AB．
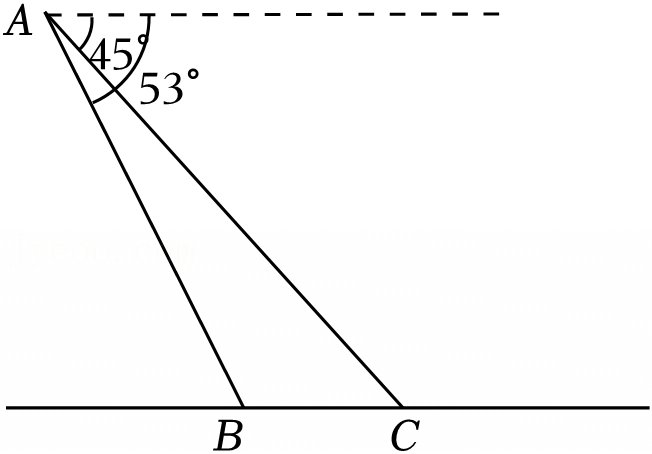
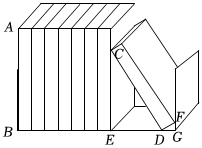如图，一个书架上放着8个完全一样的长方体档案盒，其中左边7个档案盒紧贴书架内侧竖放，右边一个档案盒自然向左斜放，档案盒的顶点D在书架底部，顶点F靠在书架右侧，顶点C靠在档案盒上，若书架内侧BG的长为60cm,∠DFG=53°，ED长度约为21cm.求出该书架中最多能竖放几个这样的档案盒．（点A、点B、点C、点D、点E、点F、点G在同一平面内．参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈0.75）
米，点B到地面的距离为2米，点C与点B的水平距离为3米，点O与水池边缘的距离OE为12米．
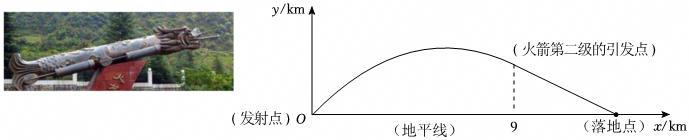
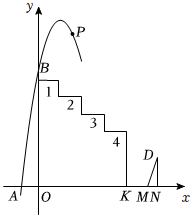如图是一个动画设计示意图，x轴上依次有A，O，K、M、N五个点．在OK上方有四个台阶1，2，3，4，每个台阶均平行于x轴，且水平宽度均为2，各个拐角为90°，相邻两个台阶的竖直距离均为2，第1个台阶到x轴距离OB=11．如图，MD为一个可以移动的斜坡，DN⊥x轴，DN=3，MN=1．从点A处向右上方沿抛物线L：y=-x2+4x+12发出一个带光点P．
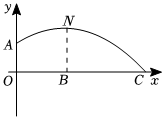这条经过A、N、C三点的抛物线是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的路径图．其中A点离地面1.4米，N点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是足球第一次落地的地点．那么足球第一次落地点C距守门员的水平距离为多少米？
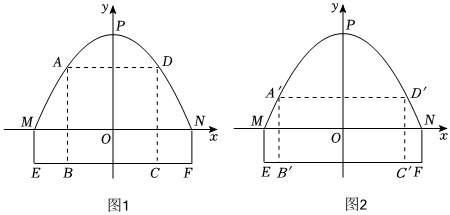
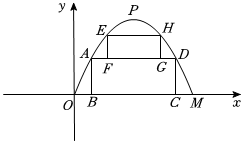白鹿原隧道被称为“中国最大断面黄土隧道”，它的截面近似看作抛物线，某数学课题学习小组，为了研究隧道的截面，建立如图坐标系，已知隧道的净宽OM约为18米，净高（即抛物线最高点到地面的距离）约为12米．在隧道施工过程中，需要一个“凸”字形的支架支撑隧道的顶部，支架的下部分和上部分都分别由矩形ABCD和矩形EFGH组成，已知下部分矩形的长BC=12米，上部分矩形的长宽比（即EH：GH=3：2），点A、D、E、H都在抛物线上．根据以上信息解决问题．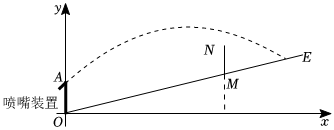
，
，
）
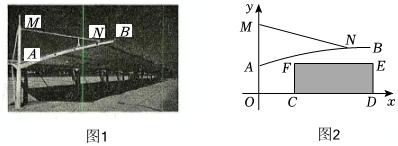
| 制作简易水流装置 | |
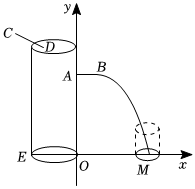
| 设计方案 | 如图，CD是进水通道，AB是出水通道，OE是圆柱形容器的底面直径，从CD将圆柱形容器注满水，内部安装调节器，水流从B处流出且呈抛物线型．以点O为坐标原点，EO所在直线为x轴，OA所在直线为y轴建立平面直角坐标系xOy,水流最终落到x轴上的点M处． |
| 示意图 |
|
| 已知 | AB∥x轴，AB=5cm,OM=15cm,点B为水流抛物线的顶点，点A、B、O、E、M在同一平面内，水流所在抛物线的函数表达式为y=ax2+bx+15（a≠0）． |
| 任务一 | 求水流抛物线的函数表达式； |
| 任务二 | 现有一个底面半径为3cm,高为11cm的圆柱形水杯，将该水杯底面圆的圆心恰好放在M处，水流是否能流到圆柱形水杯内？请通过计算说明理由．（圆柱形水杯的厚度忽略不计） |
dyczsxyn
2025-06-14
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
如图，灌溉车为绿草地浇水，以点O为坐标原点，OC所在直线为x轴，OH所在直线为y轴，喷水口H离地竖直高度OH为1.2米，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象，下边缘抛物线可由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2米，高出喷水口0.4米．