模型建立如图在等腰直角三角形中直线经过点过点作于点过点作于点请直接写出图中相等的线段除模型应用如图在平面直角坐标系中直线与轴分别交于两点为第一象限内的点若是以为直角边的等腰直角三角形请求出点的坐标和直线的表达式探究提升如图在平面直角坐标系中点在轴上运动将绕点顺时针旋转至连接求

首页 > 试题列表 > 单题解析

180199. （2023•唐南中学•八上二月）（1）模型建立：
如图1，在等腰直角三角形ABC中，∠ACB＝90°，CA＝CB，直线ED经过点C，过点A作AD⊥ED于点D，过点B作BE⊥ED于点E，请直接写出图中相等的线段（除CA＝CB）；
模型应用：
（2）如图2，在平面直角坐标系xOy中，直线

与x，y轴分别交于A、B两点，C为第一象限内的点，若△ABC是以AB为直角边的等腰直角三角形，请求出点C的坐标和直线BC的表达式；
探究提升：
（3）如图3，在平面直角坐标系xOy中，A（3，0），点B在y轴上运动，将AB绕点A顺时针旋转90°至AC，连接OC，求CA+OC的最小值，及此时点B坐标．

共享时间:2023-12-22 难度:5

纠错

下载

相似

组卷

[考点]

一次函数综合应用，

[答案]

见试题解答内容

[解析]

（1）解：∵∠ACB＝90°，
∴∠ACD+∠BCE＝90°．
∵AD⊥ED，BE⊥ED，
∴∠D＝∠E＝90°，
∴∠ACD+∠CAD＝90°，
∴∠CAD＝∠BCE，
∵CA＝CB，
∴△ACD≌△CBE（AAS），
∴AD＝CE，CD＝BE．
（2）以点A为直角顶点时，如图，作CD⊥OA于点D．

∵

，
∴x＝0时，y＝8；当y＝0时，x＝6，
∴A（6，0），B（0，8）．
∵∠CAB＝90°，
∴∠CAD+∠BAO＝90°．
∵CD⊥OA，
∴∠AOB＝∠ADC＝90°，
∴∠ACD+∠CAD＝90°，
∴∠ACD＝∠BAO，
∵CA＝AB，
∴△ACD≌△BAO（AAS），
∴AD＝OB＝8，CD＝OA＝6，
∴OD＝6+8＝14，
∴C（14，6）．
设直线BC的解析式为y＝kx+8，把C（14，6）代入，得14k+8＝6，
∴

，
∴

；
当以点B为直角顶点时，作CD⊥OB于点D．如图，

同理可求：CD＝OB＝8，BD＝OA＝6，
∴OD＝6+8＝14，
∴C（8，14）．
设直线BC的解析式为y＝nx+8，把C（8，14）代入，得8n+8＝14，
∴

，
∴

．
（3）如图，过点C作CD⊥OA轴于点D，设OB＝t．

∵∠CAB＝90°，
∴∠CAD+∠BAO＝90°．
∵CD⊥OA，
∴∠AOB＝∠ADC＝90°，
∴∠ACD+∠CAD＝90°，
∴∠ACD＝∠BAO，
∵CA＝AB，
∴△ACD≌△BAO（AAS），
∴AD＝OB＝t，CD＝OA＝3，
∴OD＝t﹣3，
∴C（3﹣t，3），
∴CA+OC＝

，
设P（t，0），M（0，3），N（3，3），
则求

的最小值可看作点P到点M和点N的距离之和最小，如图，

作点M（0，3）关于x轴的对称点M'（0，﹣3），连接M'N交x轴于点P，连接MP，
则PM+PN＝PM'+PN＝M'N＝

．
设直线M'N的解析式为y＝mx﹣3，把N（3，3）代入得3m﹣3＝3，
∴m＝2，
∴y＝2x﹣3，
当y＝0时，

，
∴

，
∴此时

，
∴

．

[点评]

本题考查了""，属于"压轴题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

193033. （2023•西安二十三中•八上二月） $德优题库$ 如图，直线l₁：y=kx+1与x轴交于点D，直线l₂：y=-x+b与x轴交于点A，且经过定点B（-1，5），直线l₁与l₂交于点C（2，m）．
（1）求k、b和m的值；
（2）求△ADC的面积；
（3）在x轴上是否存在一点E，使△BCE的周长最短？若存在，请求出点E的坐标；若不存在，请说明理由．

共享时间:2023-12-29 难度:5 相似度:2

解析

纠错

下载

组卷

181298. （2023•西航一中•八上二月）如图，在平面直角坐标系中，A、B、C为坐标轴上的三个点，且OA＝OB＝OC＝6，过点A的直线AD交直线BC于点D，交y轴于点E，△ABD的面积为18．
（1）求点D的坐标．
（2）求直线AD的表达式及点E的坐标．
（3）过点C作CF⊥AD，交直线AB于点F，求点F的坐标．

共享时间:2023-12-23 难度:5 相似度:2

解析

纠错

下载

组卷

179202. （2024•西安湖滨中学•八上期中）学完勾股定理的证明后发现运用“同一图形的面积有两种不同的表示方式”可以证明一类含有线段的等式，这种解决问题的方法我们称之为等面积法．
（1）【学有所用】如图1，在等腰△ABC中，AB＝AC，其一腰上的高BD为h，M是底边BC上的任意一点，M到腰AB、AC的距离ME、MF分别为h₁、h₂，小明发现，通过连接AM，将△ABC的面积转化为△ABM和△ACM的面积之和，建立等量关系，便可证明h₁+h₂＝h，请你结合图形来证明：h₁+h₂＝h；
（2）【尝试提升】如图2，在△ABC中，∠A＝90°，D是AB边上一点，使BD＝CD，过BC上一点P，作PE⊥AB，垂足为点E，作PF⊥CD，垂足为点F，已知

，

，求PE+PF的长；
（3）【拓展迁移】如图3，在平面直角坐标系中有两条直线l₁：

，l₂：y＝5x﹣5，若l₂上的一点M到l₁的距离是2，请直接写出符合题意的M点坐标　．

共享时间:2024-11-21 难度:5 相似度:2

解析

纠错

下载

组卷

179507. （2024•高新一中•八上期中）我们规定：如图，点H在直线MN上，点P和点P′均在直线MN的同侧，如果HP=HP′，∠PHM=∠P′HN，点P′就是点P关于直线MN的“反射点”，其中点H为“V点”，连接PP′，称△PHP′为“反V三角形”．在平面直角坐标系xOy中： $德优题库$

（1）如果点P（0，4），H（2，0），那么点P关于x轴的反射点P′的坐标为；
（2）已知点A（0，a），过点A作平行于x轴的直线l.如果点B（5，3）关于直线l的反射点B′和“V点”都在直线y=-x+4上，求点B′的坐标和a的值；
（3）如果点P为直线y=2x-4上一点，点P关于直线y=2的反射点为P′，点H为V点，如果反V△PHP′为直角三角形，且面积为8，求反射点P′的坐标．

共享时间:2024-11-25 难度:5 相似度:2

解析

纠错

下载

组卷

179607. （2024•高新一中•八上期中）如图1，已知直线y＝﹣3x+6与x轴、y轴交于A、B两点，过点B的直线y＝x+6与x轴交于点C，经过原点的直线y＝mx，与直线AB，BC分别交于点E、F．
（1）如图1，若S_△BOE＝S_△BOF，求直线EF的表达式；
（2）如图2，若直线AB与直线EF的夹角∠BEF＝45°，求m的值；
（3）如图3，将（1）中直线EF向上平行移动后经过点B，与x轴交于点G，设H为线段BG上一点（含端点），连接AH，一动点M从点A出发，沿线段AH运动到H，再沿线段HB运动到B后停止，若点M在AH上的速度为每秒1个单位，在HB上的速度为每秒

个单位，当点H的坐标是多少时，点M在整个运动过程中用时最少？

共享时间:2024-11-11 难度:5 相似度:2

解析

纠错

下载

组卷

179709. （2024•铁一中学•八上期中）如图1，在平面直角坐标系中，直线

交x轴于点A，交y轴于点B，点C与点B关于x轴对称，连接AC．
（1）C的坐标是　　；
（2）在x轴上是否存在一点D，使得△ACD是等腰三角形，若存在，求出点D坐标，若不存在，说明理由；
（3）直线x＝a（a≠﹣4）交直线AC于点E、交直线AB于点F，点Q为y轴上的一个动点，△QEF为等腰直角三角形，请直接写出a的值．

共享时间:2024-11-13 难度:5 相似度:2

解析

纠错

下载

组卷

181057. （2023•华山中学•八上二月）如图，直线l_AB：y＝﹣

的图象与x轴和y轴分别交于点A和点B，将△AOB沿直线l对折使点A和点B重合，直线l与x轴交于点C，与AB交于点D，连接BC．
（1）求线段OC的长；
（2）若点E是点C关于y轴的对称点，求△BED的面积；
（3）已知y轴上有一点P，若以点B，C，P为顶点的三角形是等腰三角形，请求出所有满足条件的点P的坐标．

共享时间:2023-12-23 难度:5 相似度:2

解析

纠错

下载

组卷

181228. （2023•爱知中学•八上二月）如图，在平面直角坐标系中，直线y＝2x+6与x轴、y轴分别交于点A、C，经过点C的直线与x轴交于点B（6，0）．

（1）求直线BC对应的函数表达式．
（2）如图①，点G是线段BC上一点，且点G满足

，求点G的坐标．
（3）如图②，点P是第二象限内一点，当△ACP是以AC为直角边的等腰直角三角形时，求点P的坐标．

共享时间:2023-12-18 难度:5 相似度:2

解析

纠错

下载

组卷

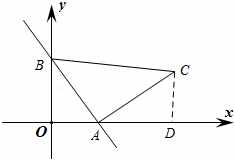
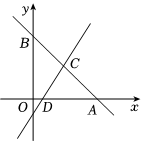181252. （2024•西光中学•八下二月） $德优题库$ 如图，在平面直角坐标系中，直线y=-x+8分别交两坐标轴于点A、B，直线CD与直线AB交于点C，与x轴交于点D，点D的坐标为（1，0），点C的横坐标为4．
（1）求直线CD的函数解析式：
（2）在坐标平面内是否存在这样的点F，使以A、C、D、F为顶点的四边形为平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．

共享时间:2024-06-24 难度:5 相似度:2

解析

纠错

下载

组卷

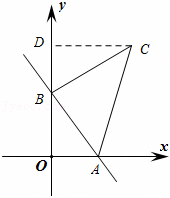
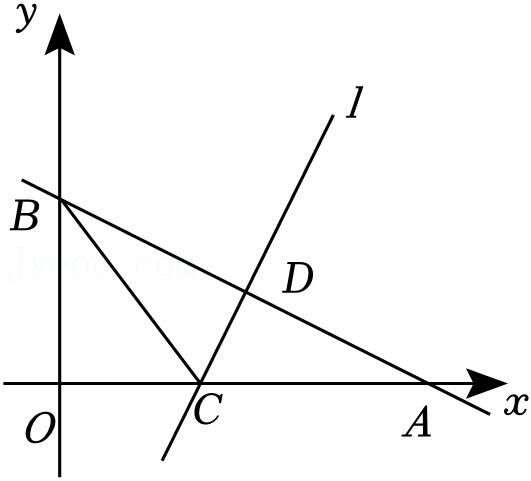
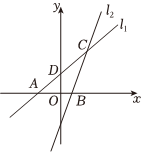181567. （2024•曲江一中•八下二月） $德优题库$ 如图，在平面直角坐标系xOy中，直线l₁：y=x+2与x轴交于点A，与y轴交于点D，直线y=4x向下平移4个单位长度得到直线l₂，直线l₂与x轴交于点B，与l₁相交于点C．
（1）直线l₂的解析式为；
（2）求点C的坐标；
（3）在坐标平面内是否存在一点N，使以A、B、C、N为顶点的四边形是平行四边形？若存在，直接写出点N的坐标；若不存在，说明理由．

共享时间:2024-06-21 难度:5 相似度:2

解析

纠错

下载

组卷

175338. （2024•西安三中•八上二月）（1）问题解决：如图1，平面直角坐标系中，直线l：y=-2x+4与x轴交于点A，与y轴交于点B，以AB为腰在第一象限作等腰直角△ABC，∠BAC=90°，点A的坐标为，点B的坐标为．
（2）求（1）中点C的坐标．
（3）类比探究
如图②，平面直角坐标系中，线段MN在x轴上，点M坐标为（-4，0），点N与M关于y轴对称，点A是线段MN上的一个动点，B点坐标为（0，4），以点A为直角顶点，AB为直角边在AB右侧作等腰直角△ABC，连接OC，在点A的运动过程当中，线段OC是否存在最小值，若存在，求出这个最小值；若不存在，请说明理由．
$德优题库$

共享时间:2024-12-22 难度:5 相似度:2

解析

纠错

下载

组卷

181591. （2023•曲江一中•八上二月）问题发现：
如果一条直线把个平面图形的面积分成相等的两部分，我们把这条直线称为这个平面图形的面积等分线．
问题探究
（1）如图1，在平面直角坐标系中，直线

与x轴和y轴分别交于A、B两点，D为线段AB上的一点且OD平分△AOB的面积，则D点坐标　（2，1）　．
（2）如图2，在四边形ABCD中，C与原点重合，D（0，4），A（﹣2，4），B（﹣6，0），点P是AB的中点，点Q在CD上，当PQ是四边形ABCD的一条面积等分线时，求Q点坐标，并求出直线PQ的表达式．
问题解决
（3）如图3，在平面直角坐标系中，长方形ABCD是神奇农场的种植园，A与原点重合，D、B分别在x轴、y轴上，其中AB＝12，BC＝20，出入口E在边AD上，且AE＝4，拟在边BC、AB、CD、上依次再找一个出入口F、G、H，沿EF、GH修两条笔直的道路（路的宽度不计）将种植园分成四块，在每一块内各种植一种蔬菜，并要求四种蔬菜的种植面积相等．请你求出此时F、G、H三点的坐标．

共享时间:2023-12-10 难度:5 相似度:2

解析

纠错

下载

组卷

189890. （2025•高新一中•八上期末）菲菲同学在数学兴趣小组中探究了这样一个折叠问题：
（1）如图①，在平面直角坐标系中，点A、B（0，4）分别是坐标轴上的两点，当∠BAO=30°时，将△AOB沿边AB翻折得到△ABC，点O的对应点为C，则点C的坐标为；
（2）如图②，点E为平面直角坐标系内一点，过E作ED⊥x轴于点D，点B为y轴上一点，点A为线段OD上一动点，将△AOB沿AB翻折得到△ABC，且E（16，17），B（0，5），当点C落在BE的连线上时，试求AE所在直线的函数表达式；
（3）如图③，菲菲同学来到一家工厂，恰逢工厂师傅正在进行某一零件的剪裁，正好遇到了一个问题需要她的帮助：四边形OBED是该零件平面示意图的一部分，A，C分别是OD，BE上两点，且∠AOB=∠ACB=∠ODE=90°，OB=BC=2dm,OD=DE=8dm,现准备在DE边上确定一点F，画出一条分割线CF，使得CF平分四边形ADEC的面积，若存在点F，请求出EF的长度，若不存在，请说明理由．
$德优题库$

共享时间:2025-02-07 难度:5 相似度:2

解析

纠错

下载

组卷

189993. （2025•新城区•八上期末）如图，在平面直角坐标系中，直线l₁：y＝kx+b（k≠0）与直线l₂：y＝3x交于点A（1，a），与y轴交于点B，与x轴交于点C（

，0）．
（1）求直线l₁的函数表达式；
（2）方程组

的解为　　；
（3）在直线l₂上是否存在一点P，使得S_△OCP＝2S_△AOC，若存在，请求出点P的坐标；若不存在，请说明理由．

共享时间:2025-02-13 难度:5 相似度:2

解析

纠错

下载

组卷

190092. （2025•西咸新区•八上期末）如图，直线l₁与x轴、y轴分别交于点A、点B（0，1），直线l₂：y=-x+4与x轴、y轴分别交于点C、点D，直线l₁与l₂交于点E（2，m）．
（1）求m的值和直线l₁的表达式；
（2）点G是x轴上的一个动点，连接GB，GE，求GB+GE的最小值和此时点G的坐标；
（3）在直线CD上是否存在一点P，使得△BEP的面积等于5，若存在，请求出点P的坐标；若不存在，请说明理由．
$德优题库$

共享时间:2025-02-08 难度:5 相似度:2

解析

纠错

下载

组卷

dyczsxyn

2023-12-22

初中数学 | 八年级上 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2023-2024学年陕西省西安市雁塔区唐南中学八年级（上）第二次月考数学试卷

更新:2023-12-22 10:37浏览量:22

普通登录

手机登录

微信扫码立即登录