服务热线
搜题▪组卷
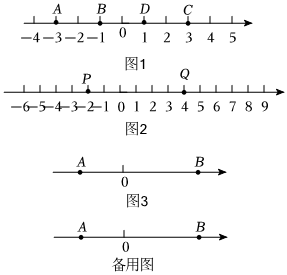 科技创新强国有我,西安滨河学校机器人社团小乐同学,在学完数轴后,他想对数轴进行深入探究,于是在机器人选修课上编写了一道与数轴相关的程序,让数学走进生活,让数学走进科技创造,他是这样设计的:
科技创新强国有我,西安滨河学校机器人社团小乐同学,在学完数轴后,他想对数轴进行深入探究,于是在机器人选修课上编写了一道与数轴相关的程序,让数学走进生活,让数学走进科技创造,他是这样设计的:


| 第一次 | 第二次 | 第三次 | |
| 手续费/元 | 0 | 1.1 | 0.2 |
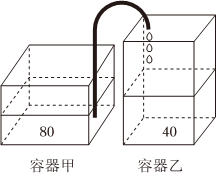 如图,甲、乙两个长方体容器放置在同一水平桌面上,容器甲的底面积为80dm2,高为6dm;容器乙的底面积为40dm2,高为9dm.容器甲中盛满水,容器乙中没有水,现从容器甲向容器乙匀速注水,每分钟注水30dm3.
如图,甲、乙两个长方体容器放置在同一水平桌面上,容器甲的底面积为80dm2,高为6dm;容器乙的底面积为40dm2,高为9dm.容器甲中盛满水,容器乙中没有水,现从容器甲向容器乙匀速注水,每分钟注水30dm3.| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度的部分 | b |


gw@dyw.com
2024-11-23
初中数学 | 八年级上 | 解答题