如图在平面直角坐标系中直线与轴交于点直线与两坐标轴分别交于点点直线与交于点点在射线上若为直角三角形则点的坐标为

首页 > 试题列表 > 单题解析

179194. （2024•西安湖滨中学•八上期中）如图，在平面直角坐标系中，直线l₁：y＝x﹣2与y轴交于点D，直线l₂与两坐标轴分别交于点A（0，2），点B（4，0），直线l₁与l₂交于点C，点P在射线DC上，若△ABP为直角三角形，则点P的坐标为　　．

共享时间:2024-11-21 难度:5

纠错

下载

相似

组卷

[考点]

一次函数综合应用，

[答案]

（6，4）或（1，﹣1）或（4，2）．

[解析]

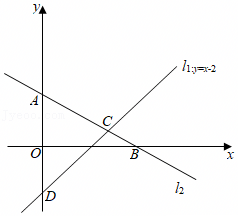
解：∵点P在射线DC上，
∴设P（p，p﹣2）（p≥0），
∵点A（0，2），点B（4，0），
∴AB²＝2²+4²＝20，PB²＝（p﹣4）²+（p﹣2）²＝2p²﹣12p+20，AP²＝p²+（p﹣2﹣2）²＝2p²﹣8p+16，
①当∠PAB＝90°时，AB²+AP²＝PB²，
∴20+2p²﹣8p+16＝2p²﹣12p+20，
∴p＝﹣4（不合题意，舍去）；
②当∠PBA＝90°时，AB²+BP²＝AP²，
∴20+2p²﹣12p+20＝2p²﹣8p+16，
∴p＝6，
∴点P的坐标为（6，4）；
③当∠APB＝90°时，AB²＝BP²+AP²，
∴20＝2p²﹣12p+20+2p²﹣8p+16，
∴p＝1或4，
∴点P的坐标为（1，﹣1）或（4，2）．
综上所述，点P的坐标为（6，4）或（1，﹣1）或（4，2）．
故答案为：（6，4）或（1，﹣1）或（4，2）．

[点评]

本题考查了""，属于"压轴题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

172581. （2024•师大附中•八上一月）若点P（﹣1，y₁）和点Q（3，y₂）是一次函数y＝（﹣k²﹣1）x+b的图象上的两点，y₁与y₂的大小关系是：y₁　　y₂（填“＞，＜或＝”）．

共享时间:2024-10-28 难度:5 相似度:2

解析

纠错

下载

组卷

dyczsxyn

2024-11-21

初中数学 | 八年级上 | 填空题

下载量
浏览量
收益额

相关试卷 更多>>

2024-2025学年陕西省西安市雁塔区铁一中湖滨学校八年级（上）期中数学试卷

更新:2024-11-21 12:38浏览量:23

普通登录

手机登录

微信扫码立即登录