服务热线
搜题▪组卷
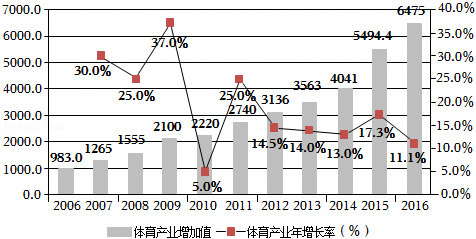
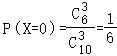 ,
,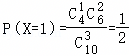 ,
, ,
,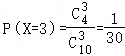 .
.| X | 0 | 1 | 2 | 3 |
| P |
| 序号i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 成绩xi(分) | 38 | 41 | 44 | 51 | 54 | 56 | 58 | 64 | 74 | 80 |
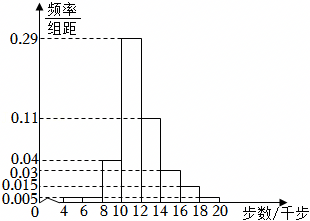
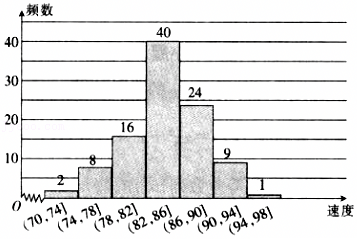
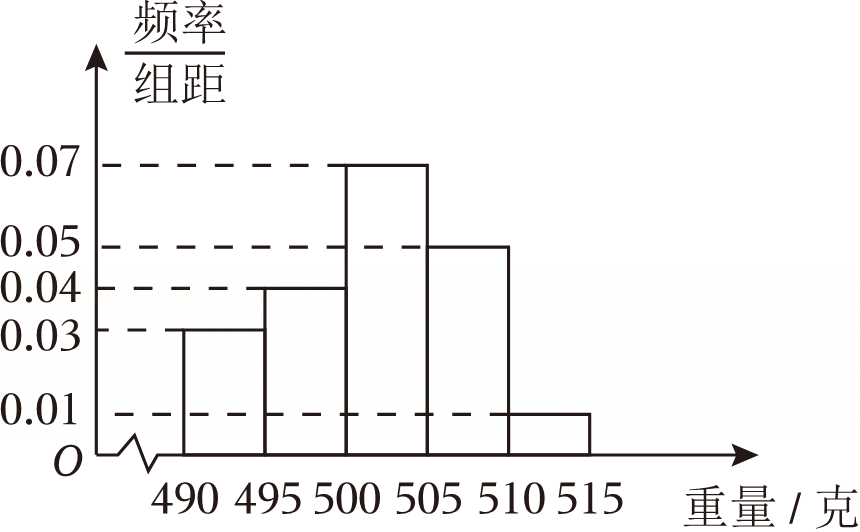
| 月份x | 1 | 2 | 3 | 4 | 5 | 6 |
| 收入y(百万元) | 6.6 | 8.6 | 16.1 | 21.6 | 33.0 | 41.0 |
| e1.52 | e2.66 | ||||||
| 3.50 | 21.15 | 2.85 | 17.50 | 125.35 | 6.73 | 4.57 | 14.30 |
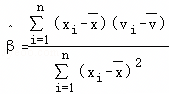 ,
,
| 组别 | 月市场需求量分组 | 频数 |
| A | 100≤x<110 | 2 |
| B | 110≤x<120 | m |
| C | 120≤x<130 | 6 |
| D | 130≤x<140 | 5 |
| E | 140≤x<150 | n |

mra@dyw.com
2022-07-08
高中数学 | 高一下 | 解答题