首页 | 客服 | 上传赚现
AI助手
德优题库AI助手

AI助手

搜题▪组卷

计算题
1道
设置组卷 进入组卷
初中数学
同步组卷 细目组卷 错题组卷 试卷组卷 中考组卷 试卷中心 共享课件 共享练考 共享学校
(1)
设置组卷 进入组卷

服务热线

400-816-0029

    自建题库，共享分红

德优题库QQ交流群

首页 > 试题列表 > 单题解析
169862. （2023•长安区一中•高一下期末） 在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC＝120°，∠ABC的平分线交AC于点D，且BD＝2，则a+2c的最小值为（　　）
A.   
B.．12       
C.． 
D.．9
共享时间:2023-07-01 难度:2
纠错 收藏 下载 相似 组卷
[考点]
正弦定理，三角形中的几何计算，
[答案]
A
[解析]
解：因为BD平分∠ABC，∠B＝120°，可得∠ABD＝∠CBD＝60°，
所以S△ABC＝acsinB＝a•BD•sin∠CBD+c•BD•∠ABD，而BD＝2，
可得ac＝2a+2c，即+＝，
所以a+2c＝2（a+2c）（+）＝2（3++），
因为a，c为三角形的边长，都为正数，由均值不等式可得a+2c≥2（3+2）＝6+4，
当且仅当＝，即a＝c时取等号，
所以a+2c的最小值为6+4．
故选：A．
[点评]
本题考查了"正弦定理，三角形中的几何计算，"，属于"易错题"，熟悉题型是解题的关键。
转载声明：
本题解析属于发布者收集录入，如涉及版权请向平台申诉！ ！版权申诉
172276. （2022•师大附中•高二下期中） 已知曲线y＝aex+xlnx在点（1，ae）处的切线方程为y＝2x+b，则（　　）
A.．a＝e，b＝﹣1               
B.a＝e，b＝1   
C.．a＝e﹣1，b＝1                
D.a＝e﹣1，b＝﹣1
共享时间:2022-05-22 难度:1 相似度:3
解析 纠错 收藏 下载 组卷
172304. （2022•师大附中•高二下期中） 在△ABC中，内角A，B，C的对边分别为a，b，c，已知c＝5，B＝，△ABC的面积为，则b＝（　　）
A.．7    
B.．7        
C.．6    
D.．6
共享时间:2022-05-16 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
169601. （2024•滨河中学•高一下期末） 在△ABC中，D为BC上一点，且，∠ABC＝∠CAD，，则tan∠ABC＝（　　）
A.     
B.      
C.      
D.．
共享时间:2024-07-23 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
172280. （2022•师大附中•高二下期中） 在△ABC中，内角A，B，C的对边分别为a，b，c，已知c＝5，B＝，△ABC的面积为，则b＝（　　）
A.7      
B.．7        
C.．6    
D.．6
共享时间:2022-05-22 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
167071. （2023•西安中学•高三上四月） 如图，在平面四边形ABCD中，△BCD是边长为7的等边三角形，AD＝3，∠BAD＝120°，则△ABC的面积为（　　）

A.     
B.      
C.    
D.
共享时间:2023-02-19 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
167182. （2023•周至四中•一模） 在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC＝120°，∠ABC的平分线交AC于点D，且BD＝2，则a+2c的最小值为（　　）
A.   
B.12        
C.
D.．9
共享时间:2023-03-04 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
169908. （2023•长安区一中•高二下期末） 在△ABC中，，则的取值范围为（　　）
A.．[﹣4，2）
B.  
C.．[﹣2，1）  
D.
共享时间:2023-07-19 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
168139. （2023•西工大附中•六模） 在△ABC中，角A，B，C的对边分别为a，b，c，若，则△ABC面积的最大值为（　　）
A.      
B.       
C.      
D.
共享时间:2023-05-19 难度:2 相似度:2
解析 纠错 收藏 下载 组卷
169775. （2023•师大附中•高二上期末） 已知△ABC三个内角A、B、C的对边分别是a、b、c，若A＝120°，b＝3，c＝8，则△ABC的面积等于（　　）
A.．6       
B.．    
C.12        
D.．
共享时间:2023-02-13 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷
170114. （2023•铁一中学•高三上期末） △ABC的内角A，B，C的对边分别为a，b，c，若a＝1，，．则c＝（　　）
A.1         
B.       
C.．     
D.．
共享时间:2023-02-08 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷
172213. （2023•西安工业大学附中•高一下期中） 一个正方体内接于一个球，过球心作一个截面，则截面不可能的图形为（　　）
A.                  
B. 
C.                  
D.．
共享时间:2023-05-16 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷
170515. （2022•高新三中•高一下期中） 在△ABC中，若a＝，b＝，∠B＝45°，则∠A的为（　　）
A.．30°或120°
B.．60°或120°
C.30°
D.60°
共享时间:2022-05-23 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷
169160. （2020•高新一中•三模） 已知△ABC中，角A，B，C所对的边分别为a，b，c，若，△ABC的面积为，则△ABC的周长为（　　）
A.8         
B.．12       
C.15        
D.
共享时间:2020-04-01 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷
171795. （2023•西安中学•高一下期中） △ABC的内角A，B，C的对边分别为a，b，c，，则（　　）

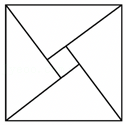
A.c＝3

B.  

C.  

D.△ABC外接圆的面积为

共享时间:2023-05-17 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷
172210. （2023•西安工业大学附中•高一下期中） 设是非零向量，若函数的图象是一条直线，则必有（　　）
A.     
B.．∥    
C.
D.
共享时间:2023-05-16 难度:1 相似度:1.5
解析 纠错 收藏 下载 组卷

dygzsxyn

2023-07-01

高中数学 | 高一下 | 选择题

  • 下载量
  • 浏览量
  • 收益额
  • 0
  • 5
  • 0
相同试题
试题下载
试题内容
调用试题名称
共享人
唐老师
试题题型
解答题
试题难度
试题题源
2020*西工大*期末
下载次数
168次
下载金币
5德优币（当前结余18德优币）
温馨提示
该试题下载至自主题库后，下载、备课永久免费！
试卷设置
试卷名称
省市校区
阶段科目
年份卷型
选择类型
已选考点
在线训练
是 否
视频讲解
温馨提示
视频讲解正在加载中、请等待！
视频解析购买
支付方式
德优币数
本次消耗0德优币
温馨提示

客服电话：400-816-0029，服务邮箱：610066832@qq.com

视频资源

试题找茬
纠错类型
纠错描述
温馨提示
共享试题、试卷经平台审核通过后方可展示，并永久享用用户下载分红权！