服务热线
搜题▪组卷
＜x＜10+
，
＝﹣2（x+
）+40≤﹣2×2
+40＝12，当且仅当x＝
，即x＝7时等号成立，
，两次购买数量之间满足关系
，记两种方案中总费用较大者与较小者的差值为数学经济值s，求该数学经济值s的最小值．
．
（万元）；年产量不小于50千件时，
（万元）．每千件商品售价为50万元．通过市场分析，该厂生产的商品能全部售完．
元（a＞0），若无论前墙的长度为多少米，乙工程队都能竞标成功，试求a的取值范围．
（k为正常数）．该商品的日销售量Q（x）（个）与时间x（天）部分数据如表所示：
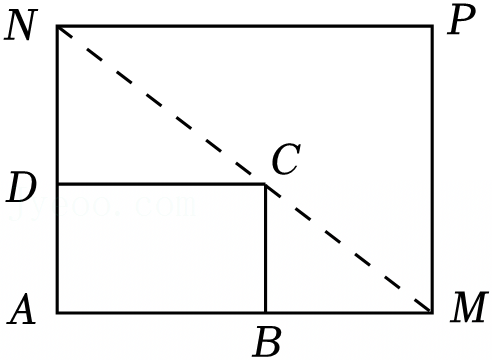
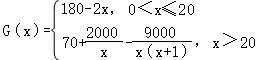| x（天） | 10 | 20 | 25 | 30 |
| Q（x）（个） | 110 | 120 | 125 | 120 |
，在区间
上单调递减，在区间
上单调递增，性质直接应用．）| x | 0 | 10 | 40 | 60 |
| Q | 0 | 1420 | 4480 | 6720 |
；
；
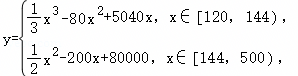且每处理一吨生活垃圾，可得到能利用的化工原料的价值为200元，若该项目不获利，政府将给予补贴．
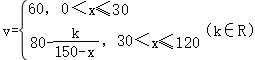．研究表明：当隧道内的车流密度达到120辆/千米时造成堵塞，此时车流速度是0千米/小时．
）
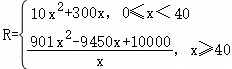．现每台产品售价为0.9万元时，当年内生产的产品当年能全部销售完．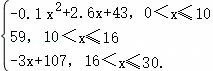
ze@dyw.com
2025-02-26
高中数学 | 高一上 | 解答题
纠错
收藏
下载
相似
组卷
解析
