服务热线
搜题▪组卷

| X | 0 | 1 | 2 |
| P |
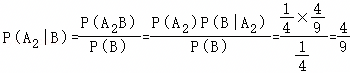 .
.| 交强险浮动因素和浮动费率比率表 | ||
| 浮动因素 | 浮动比率 | |
| A1 | 上一个年度未发生有责任道路交通事故 | 下浮10% |
| A2 | 上两个年度未发生有责任道路交通事故 | 下浮20% |
| A3 | 上三个及以上年度未发生有责任道路交通事故 | 下浮30% |
| A4 | 上一个年度发生一次有责任不涉及死亡的道路交通事故 | 0% |
| A5 | 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮10% |
| A6 | 上一个年度发生有责任道路交通死亡事故 | 上浮30% |
| 类型 | A1 | A2 | A3 | A4 | A5 | A6 |
| 数量 | 20 | 10 | 10 | 20 | 15 | 5 |
| 级数 | 全月应纳税所得额 | 税率 |
| 1 | 不超过3000元的部分 | 3% |
| 2 | 超过3000元至12000元的部分 | 10% |
| 3 | 超过12000元至25000元的部分 | 20% |
| 4 | 超过25000元至35000元的部分 | 25% |
| … | … | … |
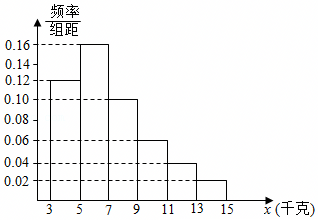
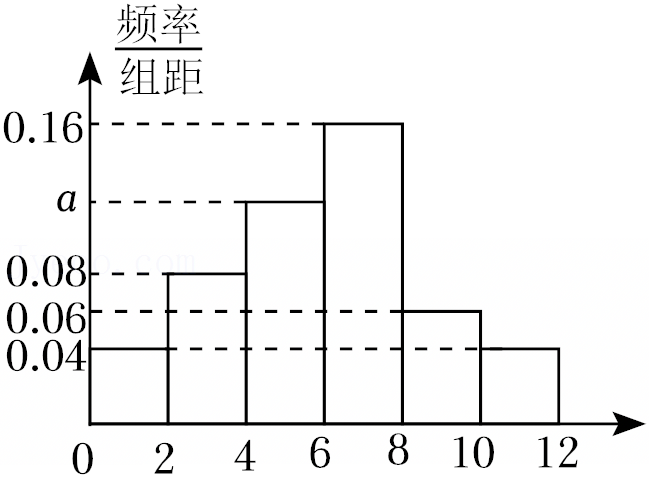
| 日均收看世界杯时间(时) | [0.5,1] | (1,1.5] | (1.5,2] | (2,2.5] | (2.5,3] | (3,3.5] |
| 频率 | 0.1 | 0.18 | 0.22 | 0.25 | 0.2 | 0.05 |
| 非足球迷 | 足球迷 | 合计 | |
| 女 | 70 | ||
| 男 | 40 | ||
| 合计 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 选考物理 | 选考历史 | 总计 | |
| 男生 | 40 | 50 | |
| 女生 | |||
| 总计 | 30 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 生产线 | [53,54) | [54,55) | [55,56) | [56,57) | [57,58) | [58,59) | [59,60] |
| 甲 | 4 | 9 | 23 | 28 | 24 | 10 | 2 |
| 乙 | 2 | 14 | 15 | 17 | 16 | 15 | 1 |
| 喜欢 | 不喜欢 | 合计 | |
| 男生 | |||
| 女生 | |||
| 合计 |
| P(K2≥k0) | 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| 生产线 | [53,54) | [54,55) | [55,56) | [56,57) | [57,58) | [58,59) | [59,60] |
| 甲 | 4 | 9 | 23 | 28 | 24 | 10 | 2 |
| 乙 | 2 | 14 | 15 | 17 | 16 | 15 | 1 |

ka@dyw.com
2024-12-24
高中数学 | 高三上 | 解答题