服务热线
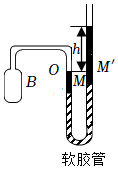如图所示是定容气体温度计的示意图，测温泡B内贮有定量的某种理想气体，经毛细管与水银压强计的左臂M相连。测温时，将B与待测系统保持热接触，上下移动压强计的右臂M'，使左臂中的水银面在不同的温度下始终固定在同一位置O处，根据此时压强计两臂水银面的高度差h和右臂上的大气压强可以求得待测温度。将温度计置于27℃的室温环境中，按照上述方法使用温度计测得高度差为4cm,大气压强为76cmHg。
小明根据气压原理设计了一个温度显示器，在烧水锅炉旁边安装一个U形细玻璃管，玻璃管的左侧与热水器相连，右侧上部封闭，并用长度为h=10cm的液态金属（密度与水银相等）封闭一段气柱，在室温27℃时，气柱长为L0=20cm,已知100℃时的饱和水蒸气压强为p汽=76cmHg,给锅炉注水后，水面上方空气的压强为一个大气压p0=76cmHg,加热后锅炉内气压为空气压强与水蒸气压强之和。求“已知27℃和80℃时饱和蒸汽压分别为3cmHg和36cmHg；且在加热过程中锅炉内水蒸气始终处于饱和状态。温度显示器内封闭气体温度与炉外室温相同”。
如图所示，U形管右管内径为左管内径的
，压力传感器示数为20N，现给洗衣缸加水，使细管中水位上升，若封闭在细管中的空气温度近似不变，当压力传感器示数为40N时，细管内水量占整条细管的比例为多少？
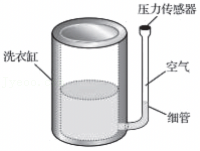
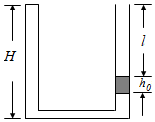如图，两侧粗细均匀、横截面积相等、高度均为H=18cm的U形管，左管上端封闭，右管上端开口。右管中有高h0=4cm的水银柱，水银柱上表面离管口的距离l=12cm。管底水平段的体积可忽略。环境温度为T1=283K，大气压强p0=76cmHg。
如图所示，一根粗细均匀、内壁光滑、竖直放置的玻璃管下端密封，上端封闭但留有一抽气孔。管内下部被活塞封住一定量的气体（可视为理想气体），气体温度为T1．开始时，活塞上方的气体的压强为p0，活塞上方玻璃管的容积为2.3V1，活塞下方气体的体积为V1，活塞因重力而产生的压强为0.5p0．缓慢将活塞上方抽成真空并密封。整个抽气过程中管内气体温度始终保持不变。然后将密封的气体缓慢加热。求：活塞刚碰到玻璃管顶部时气体的温度。
，与容器底部相距h，此时封闭气体的温度为T0，现在活塞上放置一质量与活塞质量相等的物块，再次平衡后活塞与容器底部相距
h，接下来通过电热丝缓慢加热气体，气体吸收热量Q时，活塞再次回到原初始位置。重力加速度为g，不计活塞与气缸的摩擦。求：
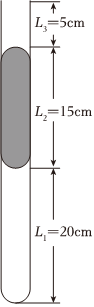如图所示，开口竖直向上的细玻璃管内有一段长为L2=15cm的水银柱，封闭了一段长度为L1=20cm的气体，此时封闭气体温度为300K，水银柱的上端距离管口的距离为L3=5cm,已知大气压强为p0=75cmHg.现把玻璃管缓慢旋转90°至水平位置保持不动，然后对玻璃管缓慢加热到水银柱刚好没流出管口，求：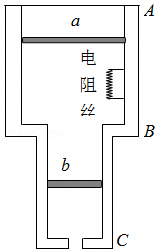
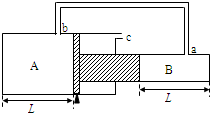，活塞b在BC的正中间。初始状态平衡，大气压强为p0，外界和气缸内气体温度均为7℃。
如图，“T”形活塞将绝热气缸内的气体分隔成A、B两部分，活塞左右两侧截面积分别为S1、S2，活塞至气缸两端底部的距离均为L，气缸上有a、b、c三个小孔与大气连通，现将a、b两孔用细管（容积不计）连接．已知大气压强为P0，环境温度为T0，活塞与缸壁间无摩擦．
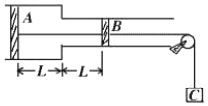如图所示，水平固定的圆筒由足够长的粗筒和细筒相接而成，筒中有直径不同的两个活塞A、B，用一根轻杆相连，活塞B通过水平细绳、定滑轮与一质量为m=2.0kg的重物C连接，A、B两活塞的横截面积分别为SA=20cm2和SB=10cm2，当两活塞封闭的空气柱温度为t1=327℃时．两活塞保持静止．此时两活塞分别与大小圆筒的相接面的距离均为L．已知大气压强为P0=1.0×105Pa.活塞与筒壁，滑轮与轮轴间的摩擦均可忽略不计．取g=10m/s2，求：
如图所示，一根粗细均匀、内壁光滑、竖直放置的玻璃管上端密封，下端封闭但留有一气孔与外界大气相连．管内上部被活塞封住一定量的气体（可视为理想气体）．设外界大气压强为p0，活塞因重力而产生的压强为0.5p0．开始时，气体温度为T1．活塞上方气体的体积为V1，活塞下方玻璃管的容积为0.5V1．现对活塞上部密封的气体缓慢加热．求：
dygzwlgr
2022-04-05
高中物理 | | 计算题
纠错
收藏
下载
相似
组卷
解析
一U形玻璃管竖直放置，左端开口，右端封闭，左端上部有一光滑的轻活塞。初始时，管内汞柱及空气柱长度如图所示。用力向下缓慢推活塞，直至管内两边汞柱高度相等时为止。求此时右侧管内气体的压强和活塞向下移动的距离。已知玻璃管的横截面积处处相同；在活塞向下移动的过程中，没有发生气体泄漏；大气压强p0=75.0 cmHg.环境温度不变。
