如图已知平分请你在横线上补充其推理过程或理由与有怎样的位置关系请说明理由若求的度数解理由因为已知所以理由因为已知所以等式的性质所以理由因为平分已知所以角平分线定义由知所以

首页 > 试题列表 > 单题解析

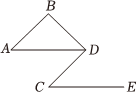244274. （2023•长安区•七下期末） $德优题库$ 如图，已知AB∥CD，DA平分∠BDC，∠A=∠C．请你在横线上补充其推理过程或理由．
（1）AD与CE有怎样的位置关系？请说明理由；
（2）若∠C=36°，求∠B的度数．
解：（1）AD∥CE．
理由：因为AB∥CD（已知），
所以∠A=       （理由：       ），
因为∠A=∠C（已知），
所以        （等式的性质），
所以AD∥CE（理由：       ）；
（2）因为DA平分∠BDC（已知），
所以∠BDA=       （角平分线定义），
由（1）知∠A=∠ADC=∠C=36°，
所以∠A=∠BDA=36°（等式性质），
因为∠A+∠B+       =180°（三角形内角和定理），
所以∠B=180°-∠A-∠BDA=       （等式的性质）．

共享时间:2023-07-13 难度:2

纠错

下载

相似

组卷白板

[考点]

平行线的判定与性质，三角形内角和定理，

[答案]

（1）∠ADC；两直线平行，内错角相等；∠ADC＝∠C；内错角相等，两直线平行；

（2）∠ADC；∠BDA；108°．

[解析]

解：（1）AD∥CE．
理由：因为AB∥CD（已知），
所以∠A＝∠ADC（理由：两直线平行，内错角相等），
因为∠A＝∠C（已知），
所以∠ADC＝∠C（等式的性质），
所以AD∥CE（理由：内错角相等，两直线平行）；
故答案为：∠ADC；两直线平行，内错角相等；∠ADC＝∠C；内错角相等，两直线平行；
（2）因为DA平分∠BDC（已知），
所以∠BDA＝∠ADC（角平分线定义），
由（1）知∠A＝∠ADC＝∠C＝36°，
所以∠A＝∠BDA＝36°（等式性质），
因为∠A+∠B+∠BDA＝180°（三角形内角和定理），
所以∠B＝180°﹣∠A﹣∠BDA＝108°（等式的性质）．
故答案为：∠ADC；∠BDA；108°．

[点评]

本题考查了"平行线的判定与性质，三角形内角和定理，"，属于"易错题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

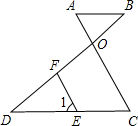24173. （2019•爱知中学•七下期中） $德优题库$ 已知，如图，AC和BD交于点O，E是CD上一点，F是OD上点，FE∥OC，∠1=∠A．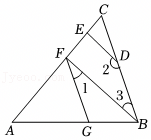
（1）试判断AB和CD的位置关系，并说明理由．
（2）若∠B=30°，∠1=65°，求∠DOC的度数．

共享时间:2019-05-05 难度:3 相似度:2

解析

纠错

下载

组卷白板

173742. （2024•经开区•八上二月）如图，在△ABC中，点D在边BC上，点G在边AB上，点E、F在边AC上，∠AGF＝∠ABC＝70°，∠1+∠2＝180°．
（1）试判断BF与DE的位置关系，并说明理由；
（2）若DE⊥AC，∠CDE＝30°，求∠A的度数．

共享时间:2024-12-17 难度:2 相似度:2

解析

纠错

下载

组卷白板

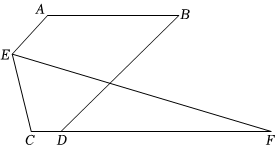189994. （2025•新城区•八上期末） $德优题库$ 如图，AE∥BD，∠A=∠BDC，∠AEC的平分线交CD的延长线于点F．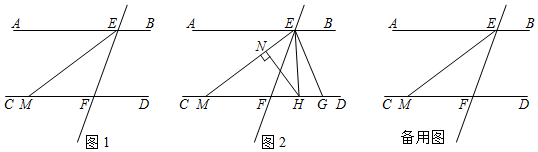
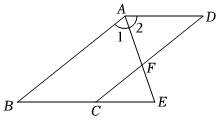【初步探索】（1）求证：AB∥CD；
【深入探索】（2）求证：∠A+∠AEC+∠C=360°；
【问题解决】（3）若∠BDC=140°，∠F=20°．求∠C的度数．

共享时间:2025-02-13 难度:2 相似度:2

解析

纠错

下载

组卷白板

24152. （2021•高新一中•七下期中）如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分∠AEF交CD于点M，且∠FEM=∠FME．
（1）猜想直线AB与直线CD有怎样的位置关系？说明你的理由；
（2）若点G为直线CD上一动点（不与点M，F重合），EH平分∠FEG交CD于点H，过点H作HN⊥EM于点N，设∠EHN=α，∠EGF=β．
①如图2，当点G在射线FD上运动时，若β=56°，求α的度数；
②当点G在直线CD上运动时，请直接写出α和β的数量关系．
$德优题库$

共享时间:2021-04-29 难度:5 相似度:1.67

解析

纠错

下载

组卷白板

185269. （2025•西安八十五中•七下期中） $德优题库$ 如图，点D，E，F分别是△ABC的边BC，CA，AB上的点，DF∥CA，∠FDE=∠A．求证：DE∥AB．

共享时间:2025-05-14 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

196405. （2024•高新一中•八上期末） $德优题库$ 如图，AB∥CD，∠B=∠D，直线EF与AD，BC的延长线分别交于点E，F，求证：∠DEF=∠F．

共享时间:2024-02-16 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185498. （2024•高新一中•七下期中） $德优题库$ 如图，AD∥BC，∠BAD的平分线交CD于点F，交BC的延长线于点E，∠B+∠BCD=180°，求证：∠CFE=∠E．
请将下面的证明过程补充完整：
证明：∵AD∥BC（已知），
∴∠2=∠E，（        ）
∴AE平分∠BAD，
∴∠1=∠2．（        ）
∴       =        .（等量代换）
∵∠B+∠BCD=180°（已知），
∴       ∥       .（        ）
∴∠1=        .（两直线平行，同位角相等）
∴∠CFE=∠E．（等量代换）

共享时间:2024-05-16 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185370. （2024•高新一中•七下期中） $德优题库$ 如图，△ABC中，AD是∠BAC的角平分线，AE是△ABC的高．若∠B=40°，∠C=62°，请说明∠DAE的度数．

共享时间:2024-05-18 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

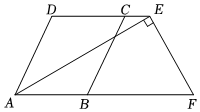185275. （2025•西安八十五中•七下期中） $德优题库$ 如图，AD∥BC，∠DCB=∠DAB，点E，F分别在直线DC，AB上，AE⊥EF．
（1）DC与AB平行吗？请说明理由；
（2）若∠DAE=∠DEA，∠DAB=60°，求∠F的度数．

共享时间:2025-05-14 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

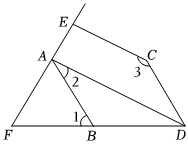244476. （2023•高新一中•八上期末） $德优题库$ 如图，已知∠1=∠BDC，∠2+∠3=180°．
（1）求证：AD∥CE；
（2）若DA平分∠BDC，DA⊥FE于点A，∠FAB=55°，求∠ABD的度数．

共享时间:2023-02-20 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185199. （2025•西工大附中•七下期中） $德优题库$ 如图，AD为△ABC的角平分线，点P为AD上的点，过点P作PE⊥AD交BC的延长线于点E．若∠B=30°，∠ACB=80°，求∠E的度数．

共享时间:2025-05-14 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

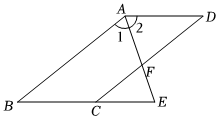185198. （2025•西工大附中•七下期中） $德优题库$ 已知：如图，AD∥BC，∠B+∠BCD=180°，∠BAD的平分线交CD于点F，交BC的延长线于点E．
求证：∠CFE=∠E．
请将下面的证明过程补充完整：
证明：∵AD∥BC（已知），
∴∠2=∠E（        ）．
∵AE平分∠BAD（已知），
∴∠1=∠2（角平分线定义）
∴∠E=∠1（        ）．
又∵∠B+∠BCD=180°（已知），
∴AB∥       （        ）．
∴∠1=        （两直线平行，同位角相等）．
∴∠CFE=∠E（等量代换）．

共享时间:2025-05-14 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

185101. （2025•铁一中学•七下期中） $德优题库$ 如图，已知AB∥CD，EG平分∠AEF，FH平分∠EFD．求证：EG∥FH．

共享时间:2025-05-15 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

181344. （2024•经开一中•七下一月） $德优题库$ 请在括号内填写理由．
如图，已知∠B+∠BCD=180°，∠B=∠D．
求证：∠E=∠DFE．
证明：∵∠B+∠BCD=180°（已知），
∴AB∥CD（       ）．
∴∠B=∠DCE（       ）．
又∵∠B=∠D（已知），
∴∠DCE=∠D（       ）．
∴AD∥BE（       ）．
∴∠E=∠DFE（       ）．

共享时间:2024-04-20 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

197033. （2024•西安八十九中•七下期末） $德优题库$ 如图，AD、AE分别为△ABC的高线和角平分线，∠B=30°，∠ACD=50°，求∠EAD的度数．

共享时间:2024-07-14 难度:1 相似度:1.5

解析

纠错

下载

组卷白板

csyn@dyw.com

2023-07-13

初中数学 | 七年级下 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2022-2023学年陕西省西安市长安区七年级（下）期末数学试卷

更新:2023-07-13 12:57浏览量:10

微信扫码立即登录

AI助手

普通登录

手机登录

微信扫码立即登录

AI助手