服务热线
搜题▪组卷
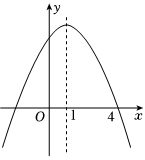已知二次函数y=ax2+bx+c（a≠0）与x轴的一个交点为（4，0），其对称轴为直线x=1，其部分图象如图所示，有下列5个结论：①abc＜0；②b2-4ac＜0；③8a+c=0；④若关于x的方程ax2+bx+c=-1有两个实数根x1x2，且满足x1＜x2，则x1＜-2，x2＞4；⑤直线y=kx-4k（k≠0）经过点（0，c），则关于x的不等式ax2+（b-k）x+c+4k＞0的解集是0＜x＜4．其中正确结论的个数为（ ）
| x | … | -1 | 0 | 1 | 2 | 5 | 6 | … |
| y | … | 11 | 4 | 1 | -4 | -1 | 4 | … |
A.关于x的一元二次方程ax2+bx+c=0有两个不等的实数根
C.a-b+c＜0
B.该二次函数有最大值
D.当x＞2时，y的值随x值的增大而增大
．
；④对于任意实数m，a+b＜am2+bm总成立；⑤关于x的方程ax2+bx+c＝n﹣1没有实数根．其中结论正确的个数为（ ）
| x | … | -1 | 0 | 1 | 2 | 5 | 6 | … |
| y | … | 41 5 |
4 | 1 | - 4 5 |
1 | 4 | … |
A.关于x的一元二次方程ax2+bx+c=0有两个不等的实数根
C.a-b+c＜0
B.该二次函数有最大值
D.当x＞2时，y的值随x值的增大而增大
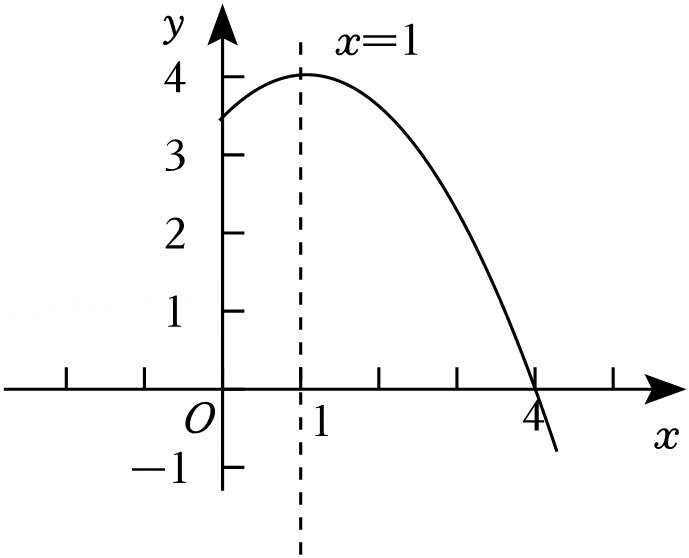
已知二次函数y=ax2+bx+c（a≠0）与x轴的一个交点为（4，0），其对称轴为直线x=1，其部分图象如图所示，有下列5个结论：①abc＜0；②b2-4ac＜0；③8a+c=0；④若关于x的方程ax2+bx+c=-1有两个实数根x1x2，且满足x1＜x2，则x1＜-2，x2＞4；⑤直线y=kx-4k（k≠0）经过点（0，c），则关于x的不等式ax2+（b-k）x+c+4k＞0的解集是0＜x＜4．其中正确结论的个数为（ ）
| x | -5 | -4 | -2 | 0 | 2 |
| y | 6 | 0 | -6 | -4 | 6 |
A.a＜0
C.当x=-2时，函数最小值为-6
B.当-4≤x＜1.5时，y＜0
D.方程ax2+bx+c+5=0有两个不相等的实数根
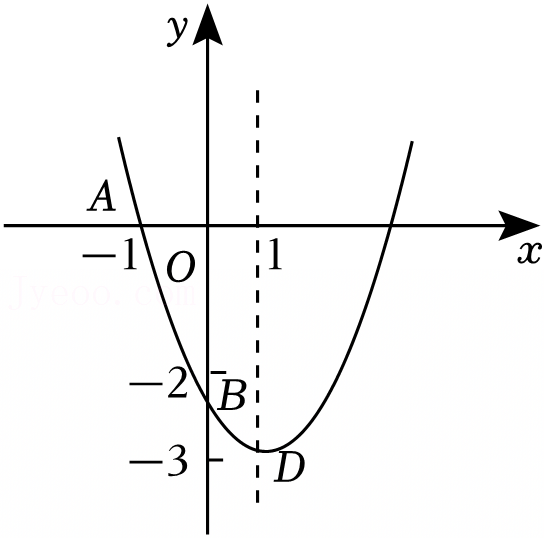
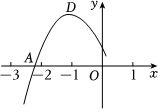抛物线y=ax2+bx+c（a≠0）的顶点为D（-1，2），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图所示，则以下结论其中正确的是（ ）
A.b2-4ac＜0
B.若方程ax2+bx+c=m没有实数根，则m≤2
C.a+b+c=0
D.若点（n-2，y1）、（n+2，y2）是抛物线上的两点（n＞1），则y1＞y2
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
A.4个
C.3个
B.2个
D.1个
A.b=2a
B.y=ax2+bx+c的最小值为-4a
C.关于x的方程ax2+bx+c=2无实数根
D.若点A（-4，y1），点B（5，y2）在y=ax2+bx+c的图象上，则y1＜y2
A.无实数根
C.有两个相等实数根
B.有两个异号实数根
D.有两个不相等实数根
A.对称轴为直线x=-1
B.当x＞0时，y随x的增大而增大
C.8a＜c
D.方程-ax2+2ax+c=-2一定有两个不相等的实数根
bjy@dyw.com
2025-02-02
初中数学 | 九年级上 | 选择题
纠错
收藏
下载
相似
组卷
解析
如图，抛物线y=ax2+bx+c与x轴交于点（-1，0），对称轴为直线x=1，则下列结论正确的是（ ）
如图为二次函数y=ax2+bx+c的图象，那么关于x的方程ax2+bx+c=-1的根的情况是（ ）
