服务热线
搜题▪组卷
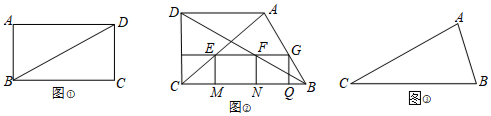
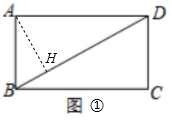
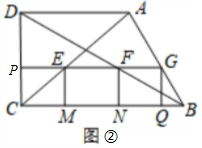
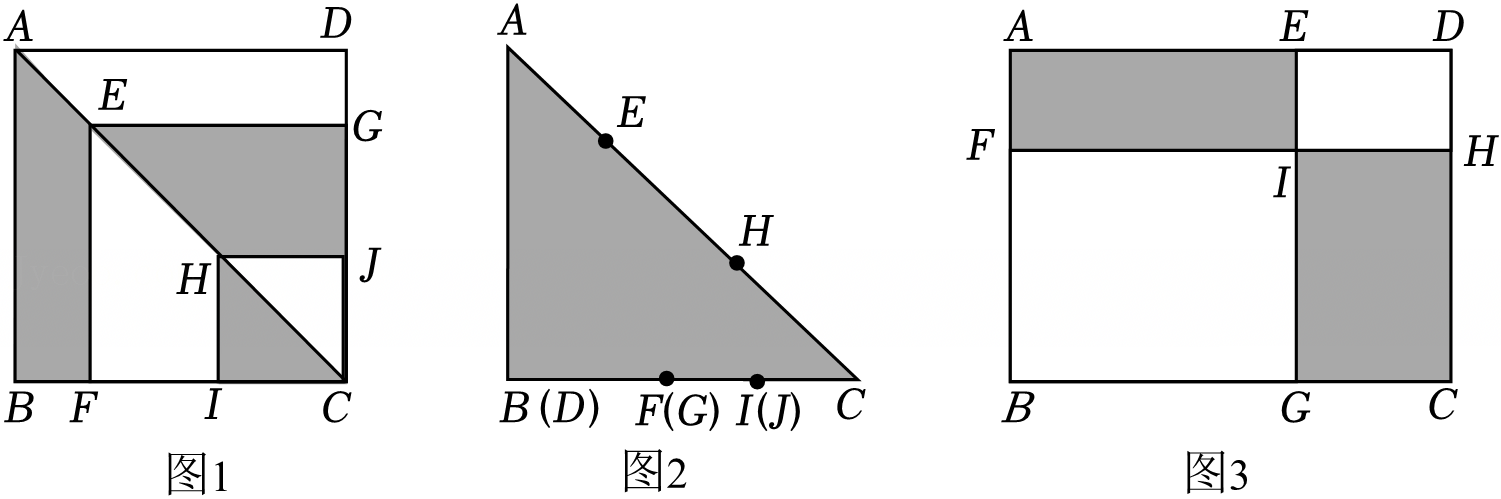
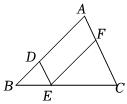 如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.
如图,在△ABC中,点D,E,F分别在AB,BC,AC边上,DE∥AC,EF∥AB.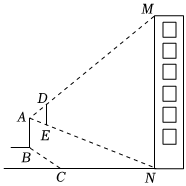 如图,小明家居住的家属楼前20米处有一土丘,经测量斜坡BC长为8米,坡角恰好为35°.一天小明站在斜坡顶端B处,手持1米的木棒ED(手臂长为0.6米,手臂与身子垂直,木棒与身子平行),发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上;眼睛A、木棒的底端E、楼房的底部N三点共线,请你计算小明家居住的这栋楼的高度.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,结果精确到1米)
如图,小明家居住的家属楼前20米处有一土丘,经测量斜坡BC长为8米,坡角恰好为35°.一天小明站在斜坡顶端B处,手持1米的木棒ED(手臂长为0.6米,手臂与身子垂直,木棒与身子平行),发现眼睛A、木棒的顶端D、楼房的顶端M在一条直线上;眼睛A、木棒的底端E、楼房的底部N三点共线,请你计算小明家居住的这栋楼的高度.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,结果精确到1米)
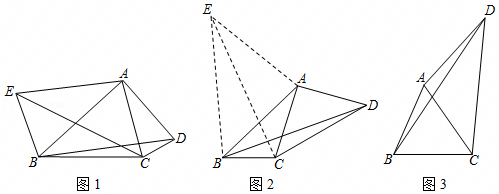
 如图,△ABC三个顶点都在格点上.
如图,△ABC三个顶点都在格点上.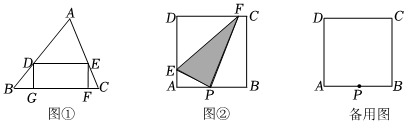
 Ων
Ων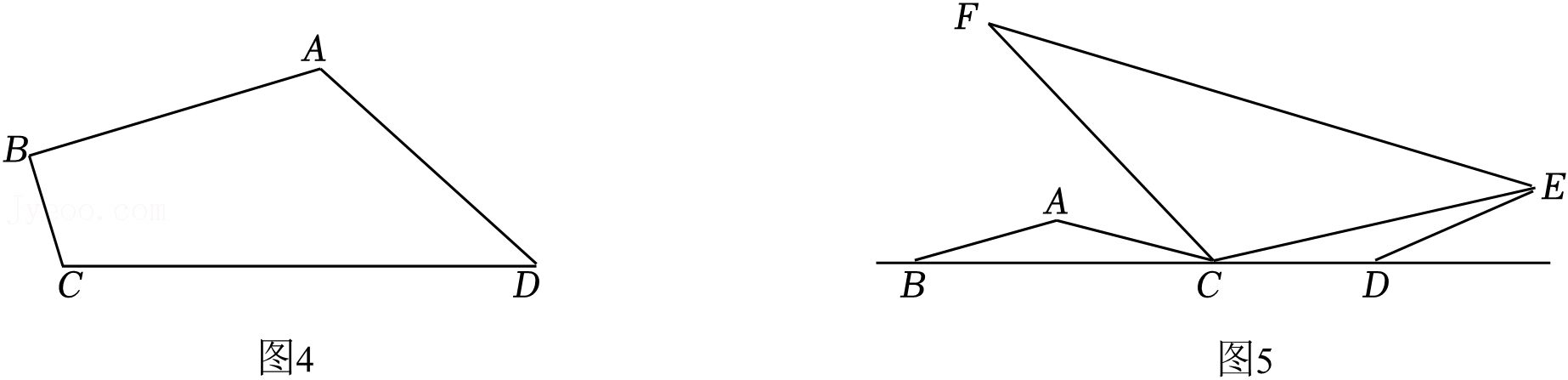
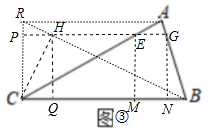
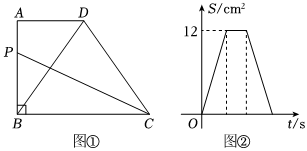 如图①,在四边形ABCD中,AD∥BC,∠B=90°,AB=4cm,BD=CD.动点P从点B出发,沿B→A→D→C的方向以每秒1cm的速度匀速运动,在整个运动过程中,△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示.
如图①,在四边形ABCD中,AD∥BC,∠B=90°,AB=4cm,BD=CD.动点P从点B出发,沿B→A→D→C的方向以每秒1cm的速度匀速运动,在整个运动过程中,△BCP的面积S(cm2)与运动时间t(s)的函数图象如图②所示.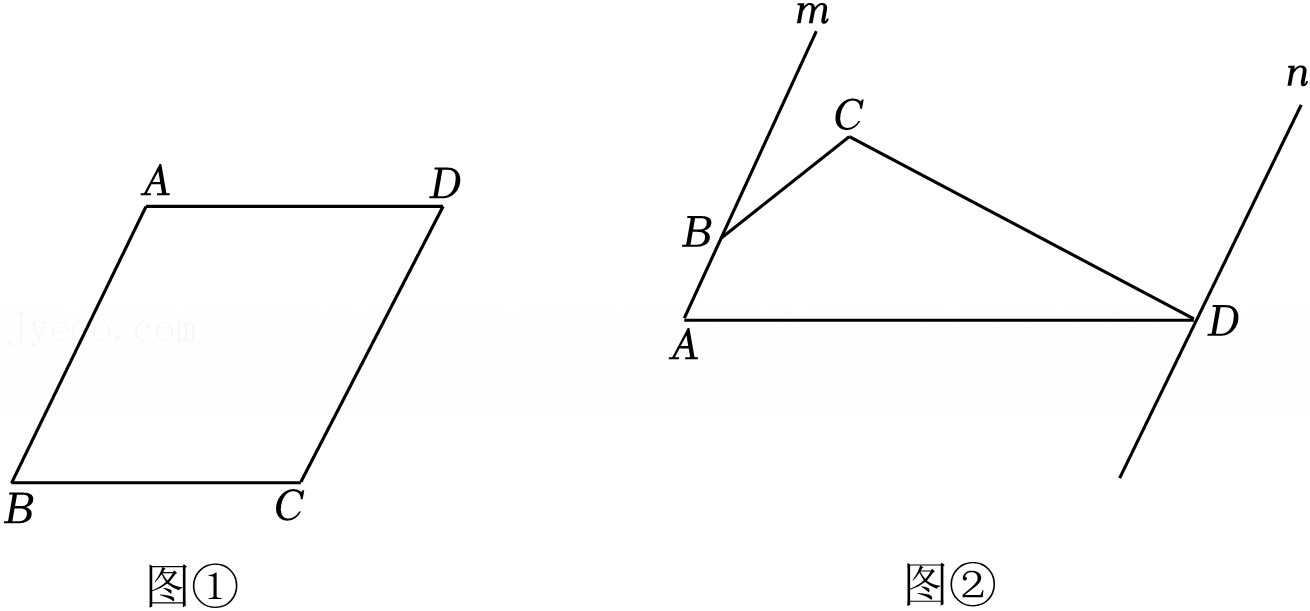

sdfz512
2017-06-08
初中数学 | | 解答题