服务热线
搜题▪组卷
约1500年前，我国伟大的数学家和天文学家祖冲之计算出圆周率应在3.1415926和3.1415927之间，成为世界上第一个把圆周率精确到小数点后7位的人．如图，若⊙O的半径为2，若用⊙O的内接正六边形的周长来估计⊙O的周长，则⊙O的周长与其内接正六边形的周长的差值为 ．（结果保留π）
＝60°，
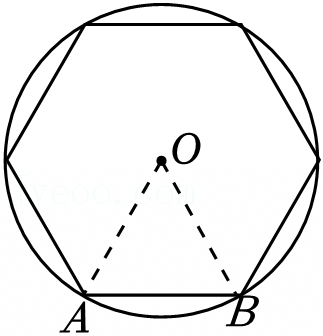
刘徽是中国古代卓越的数学家之一，他在《九章算术》中提出了“割圆术”，即用内接或外切正多边形逐步逼近圆来近似计算圆的面积．设⊙O的半径为2，若用⊙O的内接正六边形的面积来近似估计⊙O的面积，则⊙O的面积约为 （结果保留根号）．
早在1800多年前，魏晋时期的数学家刘徽首创“割圆术”，用圆内接正多边形的面积去无限逼近圆面积．如图所示的圆的内接正十二边形，若该圆的半径为1，则这个圆的内接正十二边形的面积为 ．
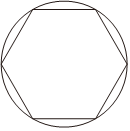我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”，即利用圆的内接正多边形逼近圆的方法来近似估算，指出“割之弥细，所失弥少．割之又割，以至于不可割，则与圆周合体，而无所失矣”．如图，⊙O的半径为1，运用“割圆术”，以圆内接正六边形面积近似估计⊙O的面积，可得π的估计值为 .（结果保留根号）
csyn@dyw.com
2024-03-15
初中数学 | | 填空题
纠错
收藏
下载
相似
组卷
解析
如图，正六边形ABCDEF的边长为2，则△ACE的周长为 ．
如图，若干全等正五边形排成环状．图中所示的是前3个正五边形，要完成这一圆环还需 个正五边形．
