服务热线
搜题▪组卷
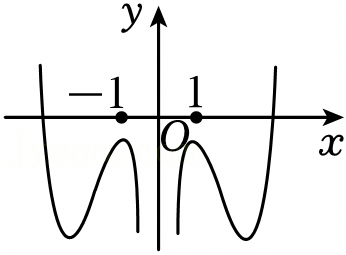
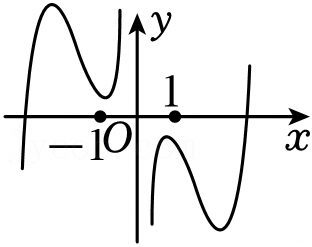
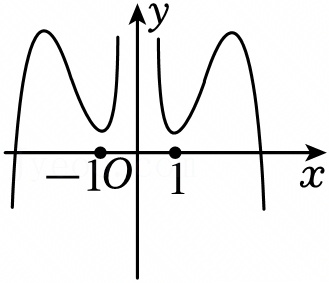
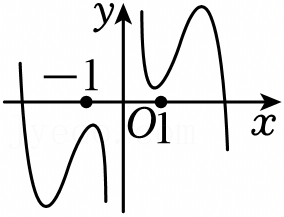
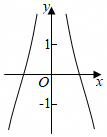
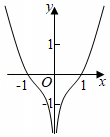
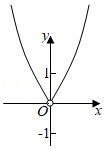
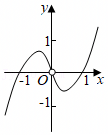
A.y=f(x)g(x)
C.![]()
B..![]()
D.![]()

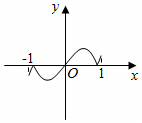
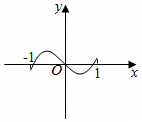
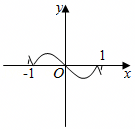
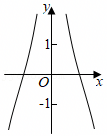
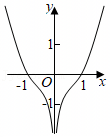
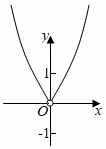
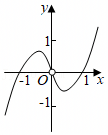
A.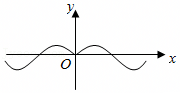
C.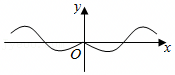
B..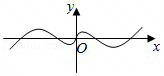
D.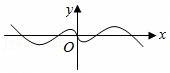
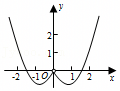
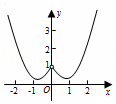
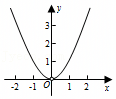
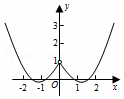
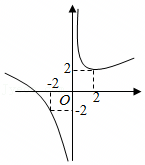
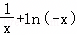
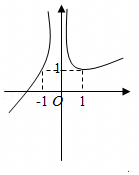
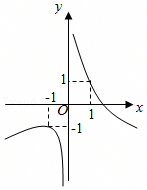
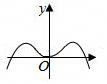
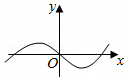
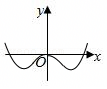
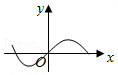
A.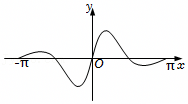
C.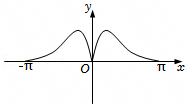
B.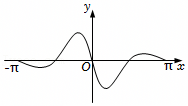
D.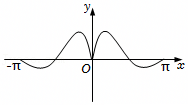

dygzsxyn
2017-02-11
高中数学 | 高二上 | 选择题