服务热线
搜题▪组卷
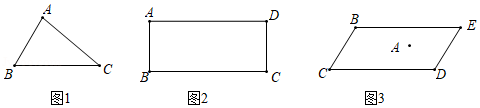
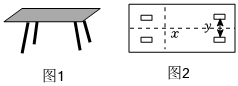 【背景阅读】图1中的板凳又叫“四脚八叉凳”,是一种传统的木制凳子,其榫卯结构体现了古人含蓄内敛的审美观.其中,榫眼的设计很有讲究,其形状为长方形,且长与宽分别与凳面的长与宽平行;木工先沿凳面的一条对称轴画一条线(如图2中虚线),再以这条线为基准向两边各取相同的长度,以确定榫眼的位置,其结构设计体现了数学的对称美.
【背景阅读】图1中的板凳又叫“四脚八叉凳”,是一种传统的木制凳子,其榫卯结构体现了古人含蓄内敛的审美观.其中,榫眼的设计很有讲究,其形状为长方形,且长与宽分别与凳面的长与宽平行;木工先沿凳面的一条对称轴画一条线(如图2中虚线),再以这条线为基准向两边各取相同的长度,以确定榫眼的位置,其结构设计体现了数学的对称美.| 以对称轴为基准向两边各取相同的长度x/mm | 16.5 | 19.8 | 23.1 | 26.4 | 29.7 |
| 凳面的宽度y/mm | 115.5 | 132 | 148.5 | 165 | 181.5 |



bs@dyw.com
2025-04-04
初中数学 | | 解答题