服务热线
搜题▪组卷
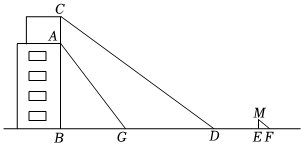数学活动实践课上，小宇和小轩所在的兴趣小组准备测量某建筑物AB顶部广告牌AC的高．测量方法如下：如图，在阳光下，某一时刻，广告牌顶端C的影子在D处，同时小宇站在E处的影长EF=2.2m,小轩在G处测得建筑物的顶端A的仰角为52°，小组其他同学测得BD=27.5m,DG=15.78m.已知小宇的身高EM=1.6m,点B，G，D，E，F在同一水平线上，且CB⊥BF，ME⊥BF．请你根据以上信息，求出广告牌AC的高．（结果精确到1m；参考数据sin52°≈0.79，cos52°≈0.62，tan52°≈1.28）
＝
，
＝
，
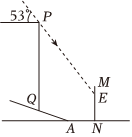（科技成就）随着5G技术的发展，为扩大网络信号的辐射范围，某通信公司在一座坡度为i=1：2.4的小山坡AQ上新建了一座大型的网络信号发射塔PQ（如图所示），信号塔底端Q到坡底A的距离为3.9米．同时为了提醒市民，在距离斜坡底A点4.4米的水平地面上立了一块警示牌：MN，当太阳光线与水平线成53°角时，测得信号塔PQ落在警示牌上的影子EN长为3米．求信号塔PQ的高．（结果精确到0.1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）
为了提高学生应用数学方法解决实际问题的能力，田老师组织学生开展了测量物体实际高度的实践活动，乐乐同学想测量公园一棵银杏树的高度AB．如图，乐乐同学站在点F处时，他在地面上的影子FG为3m,同一时刻，测得银杏树AB在平地上的影长BC为16m,在坡面的影长CD为10m,坡角为16°，其中点F，G，B，C在同一直线上．已知乐乐同学的身高EF为1.7m,则银杏树AB的高为多少米？（结果精确到0.1米，参考数据：sin16°≈0.28，cos16°≈0.96，tan16°≈0.29）
小明和小华利用学过的知识测量操场旗杆CD的高度，测量时，小明让小华站在点B处，此时，小华影子的顶端E与旗杆的影子C顶端重合，且BE的长为2米；小明又让小华沿着射线BD的方向走15.2米到达旗杆的另一侧N处，此时，小华观测到旗杆顶端C的仰角为45°，已知小华的身高为1.8米，请你根据相关测量信息，计算旗杆CD的高度．
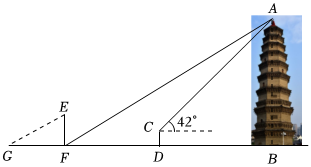小华和小明想利用测倾器和阳光下的影子来测量一座古塔的高度AB，由于古塔周围有护栏保护，他们无法到达古塔的底部B．如图所示，他们的测量方法是：首先，在阳光下，小华在古塔的影子顶端F处竖立一个标杆EF，EF的影长FG=3米，标杆EF=2米；然后，在古塔影子上的点D处安装测倾器CD，测得古塔顶端A的仰角为42°，量得CD=1米，DF=14米．已知在测量过程中，点B，D，F，G在同一水平直线上，AB，CD，EF均垂直于BG．求古塔的高度AB．（结果精确到1米，参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）
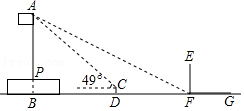
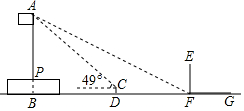小华和同学们想用一些测量工具和所学的几何知识测量学校旗杆的高度PA，检验自己掌握知识和运用知识的能力．如图所示，旗杆直立于旗台上的点P处，他们的测量方法是：首先，在阳光下，小华站在旗杆影子的顶端F处．此时，量的小华的影长FG=2m小华身高EF=1.6m；然后，在旗杆影子上的点D处，安装测频器CD．测得旗杆顶端A的仰角为49°，量得CD=0.6m,DF=5m,旗台高BP=1.2m.已知在测量过程中，点B、D、F、G在同一水平直线上，点A、P、B在同一条直线上，AB、CD、EF均垂直于BG，求旗杆的高度PA（参考数据：sin49°≈0.8，cos49°≈0.7．tan49°≈1.2）．
一天中午，小旭和小华两人想利用所学知识测量当地一座古塔的高度AB（古塔的底部不可到达），如图所示，小旭先在塔影子的顶端C处竖立长为1.5m的标杆CD，测得标杆的影长CE为2m,此时小华在标杆的影子顶端E处放置测角仪EF，测得塔顶端B的仰角为35°，已知测角仪EF的高度为1.5m,EF⊥AE，CD⊥AE，AB⊥AE，点A，C，E在同一水平直线上，求该古塔的高度AB．（参考数据：tan35°≈0.70，sin35°≈0.57，cos35°≈0.82）
如图，公园内有一个垂直于地面的立柱AB，其旁边有一个坡面CQ，坡角∠QCN=30°．在阳光下，小明观察到AB在地面上的影长为120cm,在坡面上的影长为180cm.同一时刻，小明测得直立于地面长60cm的木杆的影长为90cm（其影子完全落在地面上）．求立柱AB的高度．
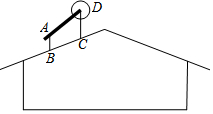如图，在屋顶的斜坡面上安装太阳能热水器：先安装支架AB和CD（均与水平面垂直），再将集热板安装在AD上．为使集热板吸热率更高，公司规定：AD与水平面夹角为θ1，且在水平线上的投影AF为140 cm.现已测量出屋顶斜面与水平面夹角为θ2，并已知tanθ1=1.082，tanθ2=0.412．如果安装工人确定支架AB高为25 cm,求支架CD的高（结果精确到1 cm）．
≈1.732）
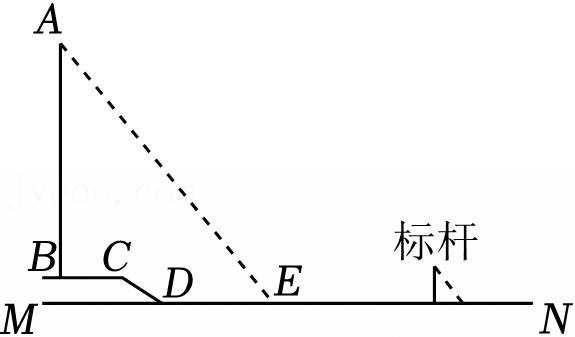
（科技成就）随着5G技术的发展，为扩大网络信号的辐射范围，某通信公司在一座坡度为i=1：2.4的小山坡AQ上新建了一座大型的网络信号发射塔PQ（如图所示），信号塔底端Q到坡底A的距离为3.9米．同时为了提醒市民，在距离斜坡底A点4.4米的水平地面上立了一块警示牌：MN，当太阳光线与水平线成53°角时，测得信号塔PQ落在警示牌上的影子EN长为3米．求信号塔PQ的高．（结果精确到0.1米，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）
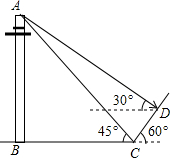如图，某学校老师们联合组织九年级学生外出开展数学活动，经过某公园时，发现工人们正在建5G信号柱，于是老师们就带领学生们对信号柱进行测量．已知信号柱直立在地面上，在太阳光的照射下，信号柱影子（折线BCD）恰好落在水平地面和斜坡上，在D处测得信号柱顶端A的仰角为30°，在C处测得信号柱顶端A的仰角为45°，斜坡与地面成60°角，CD=12米，求信号柱AB的长度．（结果保留根号）
如图，操场上的旗杆AB直立于地面．阳光明媚的一天某时刻，它的影子恰好落在地面AC和操场看台坡面CD上，科学小组的同学经过测量得知，地面上的影子AC=10.5米，看台坡面上的影子CD=18米，看台与地面的夹角∠DCE=45°，并测得同一时刻20厘米的物体在阳光下的影长是30厘米．请你根据科学小组的测量数据，计算旗杆AB的高度．（参考数据：sin45°=cos45°≈0.7）
小华想利用太阳光测量楼AB的高，他带着尺子来到楼下，发现地面和对面斜坡（坡角为45°）上都有这栋楼的影子，针对这种情况，他设计了一种测量方案，具体测量情况如下：先测得在此时刻1.2m高的物体垂直于地面放置时，影长是1m；楼AB落在地面上的影长AD=20m,落在斜坡上的影长CD=10m,请你帮小华求出楼AB的高．
陕西省西安市罗汉洞村观音禅寺内有一棵千年银杏树，据传是当年唐太宗李世民亲手栽种，距今已有1400多年历史，已被国家列为古树名木保护名录．小华是一位数学爱好者，想利用所学的知识测量这棵银杏树的高度．阳光明媚的一天，小华站在点D处利用测倾器测得银杏树顶端A的仰角为39°，然后着DM方向走了19米到达点F处，此时银杏树的影子顶端与小华的影子顶端恰好重合，小华身高EF=1.7米，测得FG=3米，测倾器的高度CD=0.8米，已知AB⊥BG，CD⊥BG，EF⊥BG．请你根据以上信息，计算银杏树AB的高度．（参考数据：sin39°≈0.6，cos39°≈0.8，tan39°≈0.8）
mt@dyw.com
2025-03-06
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
