服务热线
搜题▪组卷
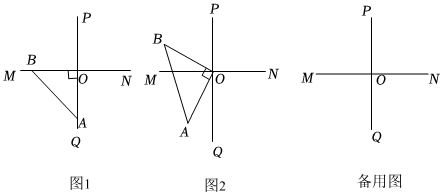
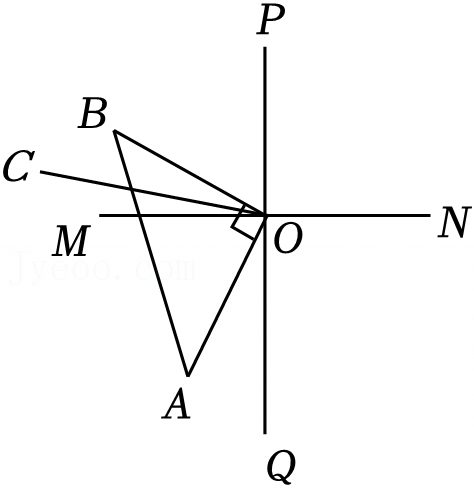
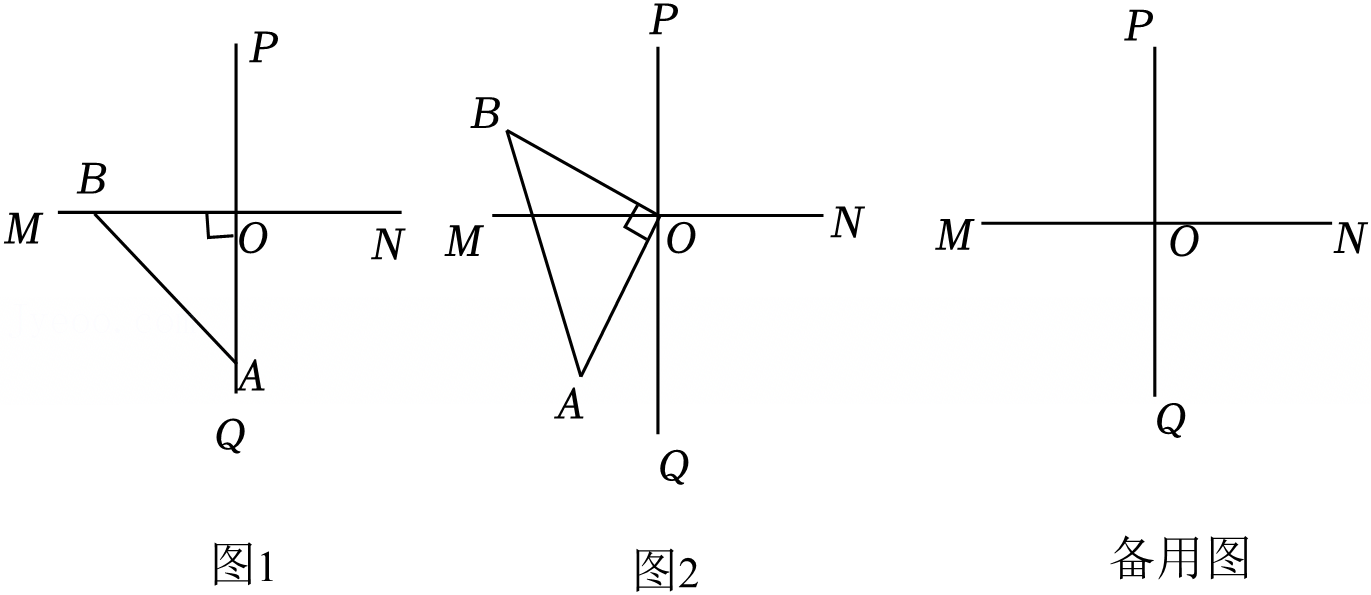
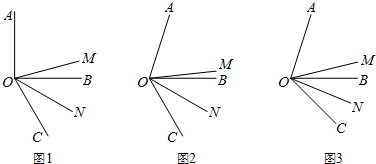
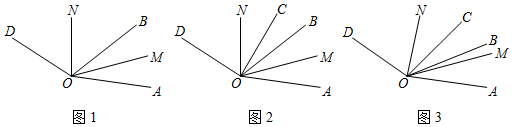
 如图,OC是∠AOD的平分线,OE是∠DOB的平分线,∠AOB=130°,∠COD=20°,求∠AOE的度数.
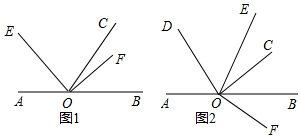
如图,OC是∠AOD的平分线,OE是∠DOB的平分线,∠AOB=130°,∠COD=20°,求∠AOE的度数.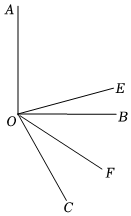 如图,在∠AOC中,射线OE平分∠AOC,点B为∠EOC内部一点,连接OB,射线OF平分∠BOC.
如图,在∠AOC中,射线OE平分∠AOC,点B为∠EOC内部一点,连接OB,射线OF平分∠BOC.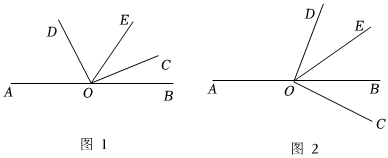
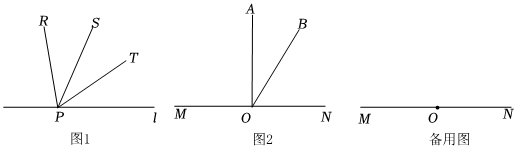
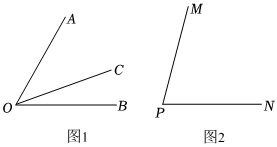 如图1,射线OC在∠AOB的内部,图中有3个角,∠AOB,∠AOC,∠BOC,若其中一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.
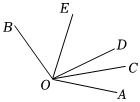
如图1,射线OC在∠AOB的内部,图中有3个角,∠AOB,∠AOC,∠BOC,若其中一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.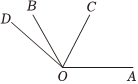 如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
如图,∠AOB=120°,射线OC从OA开始,绕点O逆时针旋转,旋转的速度为每分钟20°;射线OD从OB开始,绕点O逆时针旋转,旋转的速度为每分钟5°,OC和OD同时旋转,设旋转的时间为t(0≤t≤15).
cl@dyw.com
2025-03-01
初中数学 | 七年级上 | 解答题