服务热线
搜题▪组卷

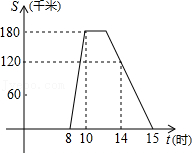
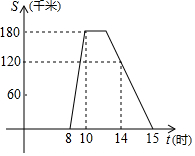 某旅游团上午8时从酒店出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离酒店的距离S(千米)与时间t(时)的关系如图所示,根据图象提供的有关信息,
某旅游团上午8时从酒店出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离酒店的距离S(千米)与时间t(时)的关系如图所示,根据图象提供的有关信息,| 月份 | 四月份 | 五月份 | 六月份 |
| 交费金额 | 30元 | 34元 | 47.8元 |
| 进价(元/盏) | 售价(元/盏) | |
| A | 30 | 45 |
| B | 50 | 70 |
| 销售单价(元/袋) | 制作成本(元/袋) | |
| 普通板栗 | 15 | 10 |
| 精品板栗 | 25 | 15 |
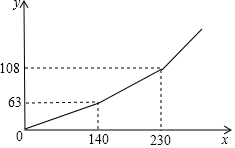
| 档次 | 第一档 | 第二档 | 第三档 |
| 每月用电量x(度) | 0<x≤140 |

shi@dyw.com
2023-12-10
初中数学 | 八年级上 | 解答题