[考点]
二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用,
[答案]
(1)11;
(2)购进A种类型的哪吒纪念娃娃590个、B种类型的哪吒纪念娃娃410个,34100.
[解析]
解:(1)设购进A种类型的哪吒纪念娃娃a个,则购进B种类型的哪吒纪念娃娃(1000﹣a)个,
根据题意,得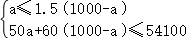 ,
解得590≤a≤600,
∵a为非负整数,
∴a取值的个数为600﹣500+1=11(个),
∴一共有11种满足条件的方案.
(2)W=(80﹣50)a+(100﹣60)(1000﹣a)=﹣10a+40000,
∴W(元)与A种类型哪吒纪念娃娃的数量a(个)之间的函数关系为W=﹣10a+40000,
∵﹣10<0,
∴W随a的减小而增大,
∵590≤a≤600且a为非负整数,
∴当a=590时W值最大,W最大=﹣10×590+40000=34100,
1000﹣590=410(个).
答:购进A种类型的哪吒纪念娃娃590个、B种类型的哪吒纪念娃娃410个可以使得总利润W最大,W的最大值为34100.
,
解得590≤a≤600,
∵a为非负整数,
∴a取值的个数为600﹣500+1=11(个),
∴一共有11种满足条件的方案.
(2)W=(80﹣50)a+(100﹣60)(1000﹣a)=﹣10a+40000,
∴W(元)与A种类型哪吒纪念娃娃的数量a(个)之间的函数关系为W=﹣10a+40000,
∵﹣10<0,
∴W随a的减小而增大,
∵590≤a≤600且a为非负整数,
∴当a=590时W值最大,W最大=﹣10×590+40000=34100,
1000﹣590=410(个).
答:购进A种类型的哪吒纪念娃娃590个、B种类型的哪吒纪念娃娃410个可以使得总利润W最大,W的最大值为34100.
[点评]
本题考查了"二元一次方程组的应用,一元一次不等式组的应用,一次函数的应用,",属于"典型题",熟悉题型是解题的关键。
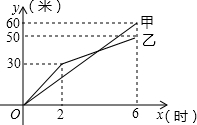
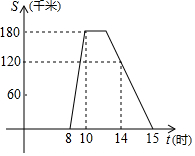 某旅游团上午8时从酒店出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离酒店的距离S(千米)与时间t(时)的关系如图所示,根据图象提供的有关信息,
某旅游团上午8时从酒店出发,乘汽车到距离180千米的某著名旅游景点游玩,该汽车离酒店的距离S(千米)与时间t(时)的关系如图所示,根据图象提供的有关信息,