已知若求不等式的解集若对任意关于的不等式恒成立求的取值范围

首页 > 试题列表 > 单题解析

172293. （2022•师大附中•高二下期中）已知f（x）＝|x+1|+|x﹣a|（a∈R）．
（1）若a＝2，求不等式f（x）＞5的解集；
（2）若对任意x∈R，关于x的不等式f（x）≥5恒成立，求a的取值范围．

共享时间:2022-05-22 难度:1

纠错

下载

相似

组卷

[考点]

绝对值不等式的解法，

[答案]

（1）（﹣∞，﹣2）∪（3，+∞）．
（2）（﹣∞，﹣6]∪[4，+∞）．

[解析]

解：（1）a＝2时，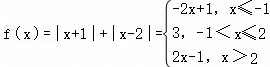

，
所以，当x≤﹣1时，不等式变为﹣2x+1＞5，解得x＜﹣2；
当﹣1＜x≤2时，不等式变为3＞5，不等式无解；
当x＞2时，不等式变为2x﹣1＞5，解得x＞3；
所以原不等式的解集为（﹣∞，﹣2）∪（3，+∞）．
（2）因为f（x）＝|x+1|+|x﹣a|≥|x+1﹣（x﹣a）|＝|a+1|，当且仅当（x+1）（x﹣a）≤0时等号成立，
所以f（x）_min＝|a+1|，
由题意知|a+1|≥5，
所以a+1≥5，或a+1≤﹣5，
所以a≥4，或a≤﹣6，
所以a的取值范围为（﹣∞，﹣6]∪[4，+∞）．

[点评]

本题考查了"绝对值不等式的解法，"，属于"基础题"，熟悉题型是解题的关键。

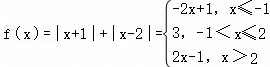转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

172399. （2022•西安中学•高二下期中）已知函数f（x）＝|2x﹣4|+|x+1|．
（1）求不等式f（x）≤6的解集；
（2）若不等式f（x）≥2a²+5a对一切实数x恒成立，求实数a的取值范围．

共享时间:2022-05-11 难度:1 相似度:2

解析

纠错

下载

组卷

168600. （2021•西安中学•九模）已知不等式|x﹣2|﹣|x﹣m|≤1对任意x∈R成立，记实数m的最小值为m₀．
（1）求m₀；
（2）已知实数a，b，c满足：a+b+2c＝m₀，a²+b²+c²＝

，求c的最大值．

共享时间:2021-06-23 难度:1 相似度:2

解析

纠错

下载

组卷

168232. （2021•西安中学•四模）已知f（x）＝（x﹣1）|x﹣a|﹣2|x﹣2|，a∈R．
（1）当a＝2时，求不等式f（x）＜0的解集；
（2）求f（2）+f（3）的最小值．

共享时间:2021-04-28 难度:1 相似度:2

解析

纠错

下载

组卷

168255. （2021•西安中学•五模）已知函数f（x）＝|x﹣2|﹣2|x|．
（1）求不等式f（x）＞1的解集；
（2）若正数a，b，c满足

，求

的最小值．

共享时间:2021-05-01 难度:1 相似度:2

解析

纠错

下载

组卷

169923. （2023•长安区一中•高二下期末）设函数f（x）＝|x﹣a²﹣2|+|x﹣a|，x∈R．
（1）当a＝2时，求不等式f（x）＞8的解集；
（2）对任意x∈R，恒有f（x）≥5﹣a，求实数a的取值范围．

共享时间:2023-07-19 难度:1 相似度:2

解析

纠错

下载

组卷

168324. （2021•西安中学•十模）已知函数f（x）＝|2x﹣a|﹣|x+1|．
（1）当a＝2时，求不等式f（x）＜1的解集；
（2）若a＞0，不等式f（x）+2＞0恒成立，求实数a的取值范围．

共享时间:2021-07-10 难度:1 相似度:2

解析

纠错

下载

组卷

168416. （2021•西安中学•十模）已知函数f（x）＝|x﹣2a|﹣2|x+a|．
（1）若f（1）≥1，求实数a的取值范围；
（2）若对任意x∈R，f（x²）≤0恒成立，求a的最小值．

共享时间:2021-07-03 难度:1 相似度:2

解析

纠错

下载

组卷

19777. （2021•陕西省•乙卷）已知函数f（x）＝|x﹣a|+|x+3|．
（1）当a＝1时，求不等式f（x）≥6的解集；
（2）若f（x）＞﹣a，求a的取值范围．

共享时间:2021-06-21 难度:4 相似度:2

解析

纠错

下载

组卷

168508. （2021•西安中学•三模）．已知函数f（x）＝|x+1|+|2x﹣1|．
（1）求不等式f（x）≥2的解集；
（2）若∃x∈[﹣1，0]，使得不等式f（x）≥a|x﹣3|成立，求实数a的最大值．

共享时间:2021-04-03 难度:1 相似度:2

解析

纠错

下载

组卷

169530. （2024•铁一中学•高三上期末）已知函数f（x）＝|a﹣x|+|x+2|．
（1）当a＝1时，求不等式f（x）≤4的解集；
（2）若f（x）＞﹣2a恒成立，求实数a的取值范围．

共享时间:2024-02-27 难度:1 相似度:2

解析

纠错

下载

组卷

168577. （2021•西安中学•九模）已知函数f（x）＝|x+1|+|x+a|．
（1）若a＝﹣4，求函数f（x）的最小值；
（2）若存在x₀∈R，使得f（x）≤|2a+3|成立，求实数a的取值范围．

共享时间:2021-06-30 难度:1 相似度:2

解析

纠错

下载

组卷

168669. （2021•西安中学•仿真）已知函数f（x）＝|x﹣4|+|x﹣1|．
（1）解不等式f（x）≤4；
（2）若方程f（x）﹣1﹣kx＝0解集为空集，求k的取值范围．

共享时间:2021-06-07 难度:1 相似度:2

解析

纠错

下载

组卷

168130. （2024•西安一中•二模）已知函数f（x）＝||x﹣2|﹣|x+1||．
（1）求f（x）的值域；
（2）求不等式

的解集．

共享时间:2024-03-17 难度:1 相似度:2

解析

纠错

下载

组卷

169421. （2024•西安中学•高三上期末）设函数f（x）＝|x+1|﹣3|x﹣1|．
（1）作出函数f（x）的图象，并求f（x）的值域；
（2）若存在x，使得不等式f（x）≥|4x﹣a|成立，求实数a的取值范围．

共享时间:2024-02-27 难度:1 相似度:2

解析

纠错

下载

组卷

169174. （2020•高新一中•三模）．已知函数f（x）＝|x+1|+|2x﹣1|．
（1）解不等式f（x）≤x+2；
（2）若g（x）＝|3x﹣2m|+|3x﹣1|，对∀x₁∈R，∃x₂∈R，使f（x₁）＝g（x₂）成立，求实数m的取值范围．

共享时间:2020-04-01 难度:1 相似度:2

解析

纠错

下载

组卷

dygzsxyn

2022-05-22

高中数学 | 高二下 | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2021-2022学年陕西师大附中高二（下）期中数学试卷（文科）

更新:2022-05-22 01:38浏览量:7

普通登录

手机登录

微信扫码立即登录