某机器生产商对一次性购买两台机器的客户推出两种超过质保期后两年内的延保维修方案方案一交纳延保金元在延保的两年内可免费维修次超过次每次收取维修费元方案二交纳延保金元在延保的两年内可免费维修次超过次每次收取维修费元某工厂准备一次性购买两台这种机器现需决策在购买机器时应购买哪种延保方案为此搜集并整理了台这种机器超过质保期后延保两年内维修的次数统计得如表维修次数机器台数以这台机器维修次数的频率代替一台机器维修次数发生

首页 > 试题列表 > 单题解析

168551. （2021•西安中学•六模）某机器生产商，对一次性购买两台机器的客户推出两种超过质保期后两年内的延保维修方案：
方案一：交纳延保金6000元，在延保的两年内可免费维修2次，超过2次每次收取维修费1500元；
方案二：交纳延保金7740元，在延保的两年内可免费维修4次，超过4次每次收取维修费a元．
某工厂准备一次性购买两台这种机器，现需决策在购买机器时应购买哪种延保方案，为此搜集并整理了100台这种机器超过质保期后延保两年内维修的次数，统计得如表：

维修次数	0	1	2	3
机器台数	20	10	40	30

以这100台机器维修次数的频率代替一台机器维修次数发生的概率．记X表示这两台机器超过质保期后延保的两年内共需维修的次数．
（1）求X的分布列；
（2）以所需延保金与维修费用之和的期望值为决策依据，该工厂选择哪种延保方案更合算．

共享时间:2021-05-15 难度:2

纠错

下载

相似

组卷

[考点]

离散型随机变量及其分布列，离散型随机变量的均值（数学期望），

[答案]

（1）

X	0	1	2	3	4	5	6
P	0.04	0.04	0.17	0.2	0.22	0.24	0.09

（2）应选择方案1．

[解析]

解：（1）根据题意，随机变量X的所有取值为0，1，2，3，4，5，6因为以这100台机器维修次数的频率代替一台机器维修次数发生的概率．
所以，P（X＝0）＝0.2×0.2＝0.04，P（X＝1）＝

×0.2×0.1＝0.04，P（X＝2）＝0.1×0.1+

＝0.17，P（X＝3）＝

＝0.2．P（X＝4）＝0.4×0.4+

＝0.22
P（X＝5）＝

＝0.24，P（X＝6）＝0.3×0.3＝0.09．
所以随机变量X的分布列为：

X	0	1	2	3	4	5	6
P	0.04	0.04	0.17	0.2	0.22	0.24	0.09

（2）设所需延保金与维修费用之和为Y_n（n＝1，2），若采用方案1，则随机变量Y₁的分布列为：

Y1	6000	7500	9000	10500	12000
p	0.25	0.2	0.22	0.24	0.09

则随机变量Y₁的期望为：E（Y₁）＝6000×0.25+7500×0.2+9000×0.22+10500×0.24+12000×0.09＝8580元．
若采用方案2，则随机变量Y₂的分布列为：

Y2	7740	a+7740	2a+7740
p	0.67	0.24	0.09

所以随机变量Y₂的期望为：
E（Y₂）＝0.67×7740+0.24×（a+7740）+0.09×（2a+7740）＝7740+0.42a元．
令7740+0.42a＝8580，得a＝2000元，
①若a＜2000，则方案1的费用高，应选择方案2．
②若a＝2000，则两种方案费用一样多，可以任选一个方案．
③若a＞2000，则方案2的费用高，应选择方案1．

[点评]

本题考查了"离散型随机变量及其分布列，离散型随机变量的均值（数学期望），"，属于"必考题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

168412. （2021•西安中学•十模）永春老醋以其色泽鲜艳、浓香醇厚的独特风味，与山西陈醋、镇江香醋、保宁药醋并称中国四大名醋．为提高效率、改进品质，某永村老醋生产公司于2018年组织技术团队进行发酵工艺改良的项目研究．2020年底，技术团队进行阶段试验成果检验，为下阶段的试验提供数据参考．现从改良前、后两种发酵工艺生产的成品醋中，各随机抽取100件进行指标值M的检测，检测分两个步骤，先检测是否合格．若合格．再进一步检测是否为一等品．因检测设备问题，改良后的成品醋有20件只进行第一步检测且均为合格，已完成检测的180件成品醋的最终结果如表所示．

指标
区间

[﹣2，﹣1）

[﹣1，0）

[0，1）

[1，2）

[2，3）

[3，4）

来源

改良
前

改良
后

改良
前

改良
后

改良
前

改良
后

改良
前

改良
后

改良
前

改良
后

改良
前

改良
后

个数

附：成品醋的品质采用指标值M进行评价．评价标准如表所示．

M∈[0，1）	M∈[1，3）	M∉[0，3）
一等品	二等品	三等品
合格		不合格

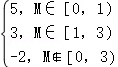（1）现从样本的不合格品中随机抽取2件，记来自改良后的不合格品件数为X，求X的分布列：
（2）根据以往的数据，每销售一件成品醋的利润y（单位：元）与指标值M的关系为y＝

，若欲实现“改良后成品醋利润比改良前至少增长20%”，则20件还未进一步检测的样本中，至少需要几件一等品？

共享时间:2021-07-03 难度:2 相似度:2

解析

纠错

下载

组卷

166643. （2024•高新一中•高三上五月）某素质训练营设计了一项闯关比赛．规定：三人组队参赛，每次只派一个人，且每人只派一次：如果一个人闯关失败，再派下一个人重新闯关；三人中只要有人闯关成功即视作比赛胜利，无需继续闯关．现有甲、乙、丙三人组队参赛，他们各自闯关成功的概率分别为p₁、p₂、p₃，假定p₁、p₂、p₃互不相等，且每人能否闯关成功的事件相互独立．
（1）计划依次派甲乙丙进行闯关，若

，

，求该小组比赛胜利的概率；
（2）若依次派甲乙丙进行闯关，则写出所需派出的人员数目X的分布，并求X的期望E[X]；
（3）已知1＞p₁＞p₂＞p₃，若乙只能安排在第二个派出，要使派出人员数目的期望较小，试确定甲、丙谁先派出．

共享时间:2024-12-26 难度:2 相似度:2

解析

纠错

下载

组卷

166756. （2024•建大附中•一模）良好的用眼习惯能够从多方面保护眼睛的健康，降低近视发生的可能性，对于保护青少年的视力具有不可替代的重要作用．某班班主任为了让本班学生能够掌握良好的用眼习惯，开展了“爱眼护眼”有奖知识竞赛活动，班主任将竞赛题目分为A，B两组，规定每名学生从A，B两组题目中各随机抽取2道题作答．已知该班学生甲答对A组题的概率均为

，答对B组题的概率均为

．假设学生甲每道题是否答对相互独立．
（1）求学生甲恰好答对3道题的概率；
（2）设学生甲共答对了X道题，求X的分布列及数学期望．

共享时间:2024-03-13 难度:2 相似度:2

解析

纠错

下载

组卷

166894. （2024•高新一中•五模）某素质训练营设计了一项闯关比赛．规定：三人组队参赛，每次只派一个人，且每人只派一次：如果一个人闯关失败，再派下一个人重新闯关；三人中只要有人闯关成功即视作比赛胜利，无需继续闯关．现有甲、乙、丙三人组队参赛，他们各自闯关成功的概率分别为p₁、p₂、p₃，假定p₁、p₂、p₃互不相等，且每人能否闯关成功的事件相互独立．
（1）计划依次派甲乙丙进行闯关，若

，

共享时间:2024-05-13 难度:2 相似度:2

解析

纠错

下载

组卷

169145. （2020•西工大附中•二模）已知三棱柱ABC﹣A₁B₁C₁中，AA₁⊥平面ABC，∠BAC＝120°，

，

，E、F分别是BC、A₁C₁的中点．
（1）证明：EF∥平面ABB₁．
（2）求直线B₁E与平面A₁BE所成角的正弦值．

共享时间:2020-03-17 难度:2 相似度:2

解析

纠错

下载

组卷

169147. （2020•西工大附中•二模）甲、乙两公司在A、B两地同时生产某种大型产品（这两个公司每天都只能固定生产10件产品），在产品发货给客户使用之前需要对产品进行质量检测，检测结果按等级分为特等品，一等品，二等品，报废品．只有特等品和一等品是合格品，且可以直接投入使用，二等品需要加以特别修改才可以投入使用，报废品直接报废，检测员统计了甲、乙两家公司某月30天的生产情况及每件产品盈利亏损情况如表所示：

	检测结果	特等品	一等品	二等品	报废品
甲公司	产品件数	210	54	20	16
乙公司	产品件数	240	18	28	14

	每件特等品	每件一等品	每件二等品	报废品
甲公司	盈2万元	盈1万元	亏1万元	亏2万元
乙公司	盈1.5万元	盈0.8万元	亏1万元	亏1.2万元

（1）分别求甲、乙两个公司这30天生产的产品的合格率（用百分数表示）．
（2）试问甲、乙两个公司这30天生产的产品的总利润哪个更大？说明理由．
（3）若从乙公司这30天生产的不合格产品中随机抽取2件产品，记抽取二等品的件数为X，求X的分布列及期望．

共享时间:2020-03-17 难度:2 相似度:2

解析

纠错

下载

组卷

169524. （2024•铁一中学•高三上期末）已知正四棱锥P﹣ABCD的底面边长和高都为2．现从该棱锥的5个顶点中随机选取3个点构成三角形，设随机变量X表示所得三角形的面积．
（1）求概率P（X＝2）的值；
（2）求随机变量X的概率分布及其数学期望E（X）．

共享时间:2024-02-27 难度:1 相似度:1.5

解析

纠错

下载

组卷

168733. （2021•西安中学•仿真） 2021年，福建、河北、辽宁、江苏、湖北、湖南、广东、重庆8省市将迎来“3+1+2”新高考模式．“3”指的是：语文、数学、英语，统一高考；“1”指的是：物理和历史，考生从中选一科；“2”指的是：化学、生物、地理和政治，考生从四科中选两科．为了迎接新高考，某中学调查了高一年级1500名学生的选科倾向，随机抽取了100人，统计选考科目人数如表：

	选考物理	选考历史	总计
男生	40		50
女生
总计		30

（Ⅰ）补全2×2列联表，并根据表中数据判断是否有95%的把握认为“选考物理与性别有关”；
（Ⅱ）将此样本的频率视为总体的概率，随机调查该校3名学生，设这3人中选考历史的人数为X，求X的分布列及数学期望．
参考公式：K²＝

，其中n＝a+b+c+d．
参考数据：

P（K²≥k₀）	0.10	0.05	0.025	0.010	0.005	0.001
k₀	2.706	3.841	5.024	6.635	7.879	10.828

共享时间:2021-06-10 难度:1 相似度:1.5

解析

纠错

下载

组卷

168778. （2021•西安中学•八模）新时代的青年应该注重体育锻炼，全面发展．为了强健学生体魄，陕西省西安中学决定全校学生参与课间健身操运动．为了调查学生对健身操的喜欢程度，现从全校学生中随机抽取了20名男生和20名女生的测试成绩（满分100分）组成一个样本，得到如图所示的茎叶图，并且认为得分不低于80分的学生为喜欢．
（1）请根据茎叶图填写下面的列联表，并判定能否有85%的把握认为该校学生是否喜欢健身操与性别有关？

	喜欢	不喜欢	合计
男生
女生
合计

（2）用样本估计总体，将样本频率视为概率，现从全校男生，女生中各抽取1人，求其中喜欢健身操的人数X的分布列及数学期望．
参考公式及数据：K²＝

，其中n＝a+b+c+d．

P（K²≥k₀）	0.150	0.100	0.050	0.025	0.010	0.001
k₀	2.072	2.706	3.841	5.024	6.635	10.828

共享时间:2021-06-19 难度:1 相似度:1.5

解析

纠错

下载

组卷

168849. （2021•西工大附中•十二模）．某市政府为了节约生活用电，计划在本市试行居民生活用电定额管理，即确定一户居民月用电量标准a，用电量不超过a的部分按平价收费，超出a的部分按议价收费．为此，政府调查了100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300）分组的频率分布直方图如图所示．
（1）根据频率分布直方图的数据，求直方图中x的值并估计该市每户居民月平均用电量μ的值；
（2）用频率估计概率，利用（1）的结果，假设该市每户居民月平均用电量X服从正态分布N（μ，σ²）
（ⅰ）估计该市居民月平均用电量介于μ～240度之间的概率；
（ⅱ）利用（ⅰ）的结论，从该市所有居民中随机抽取3户，记月平均用电量介于μ～240度之间的户数为ξ，求ξ的分布列及数学期望E（ξ）．

共享时间:2021-07-22 难度:1 相似度:1.5

解析

纠错

下载

组卷

168964. （2021•交大附中•四模）甲、乙两人进行抛硬币游戏，规定：每次抛币后，正面向上甲赢，否则乙赢．此时两个人正在游戏，且知甲再赢3次就获胜，而乙要再赢4次才获胜，其中一人获胜游戏结束．设再进行ξ次抛币后游戏结束．
（1）求概率P（ξ＝4）；
（2）求的分布列，并求其数学期望E（ξ）．

共享时间:2021-04-20 难度:1 相似度:1.5

解析

纠错

下载

组卷

169033. （2020•西安中学•三模）为迎接2022年北京冬奥会，推广滑雪运动，某滑雪场开展滑雪促销活动，该滑雪场的收费标准是：滑雪时间不超过1小时免费，超过1小时的部分每小时收费标准为40元（不足1小时的部分按1小时计算）．有甲、乙两人相互独立地来该滑雪场运动，设甲、乙不超过1小时离开的概率分别为

，

；1小时以上且不超过2小时离开的概率分别为

，

；两人滑雪时间都不会超过3小时．
（Ⅰ）求甲、乙两人所付滑雪费用相同的概率；
（Ⅱ）设甲、乙两人所付的滑雪费用之和为随机变量ξ．求ξ的分布列与数学期望E（ξ）．

共享时间:2020-04-01 难度:1 相似度:1.5

解析

纠错

下载

组卷

170392. （2022•长安区一中•高二下期末）甲、乙两个乒乓球运动员进行乒乓球比赛，已知每一局甲胜的概率为0.6，乙胜的概率为0.4，比赛时可以用三局二胜或五局三胜制，问：
（1）在哪一种比赛制度下，甲获胜的可能性大？
（2）若采用三局二胜制，求比赛场次ξ的分布列及数学期望．

共享时间:2022-07-21 难度:1 相似度:1.5

解析

纠错

下载

组卷

169919. （2023•长安区一中•高二下期末）某学校共有1000名学生参加知识竞赛，其中男生500人，为了解该校学生在知识竞赛中的情况，采取分层抽样随机抽取了100名学生进行调查，分数分布在450～950分之间，根据调查的结果绘制的学生分数频率分布直方图如图所示：将分数不低于750分的学生称为“高分选手”．
（1）求a的值，并估计该校学生分数的平均数、中位数和众数；（同一组中的数据用该组区间的中点值作代表）；
（2）现采用分层抽样的方式从分数落在[650，750），[750，850）内的两组学生中抽取8人，再从这8人中随机抽取3人，记被抽取的3名学生中属于“高分选手”的学生人数为随机变量X，求X的分布列及数学期望．

共享时间:2023-07-19 难度:1 相似度:1.5

解析

纠错

下载

组卷

170147. （2023•铁一中学•高二下期末）某企业拥有甲、乙两条零件生产线，为了解零件质量情况，采用随机抽样方法从两条生产线共抽取180个零件，测量其尺寸（单位：mm）得到如下统计表，其中尺寸位于[55，58）的零件为一等品，位于[54，55）和[58，59）的零件为二等品，否则零件为三等品．

生产线	[53，54）	[54，55）	[55，56）	[56，57）	[57，58）	[58，59）	[59，60]
甲	4	9	23	28	24	10	2
乙	2	14	15	17	16	15	1

（1）将样本频率视为概率，从甲、乙两条生产线中分别随机抽取2个零件，每次抽取零件互不影响，以ξ表示这4个零件中一等品的数量，求ξ的分布列和数学期望E（ξ）；
（2）已知该企业生产的零件随机装箱出售，每箱60个．产品出厂前，该企业可自愿选择是否对每箱零件进行检验．若执行检验，则每个零件的检验费用为5元，并将检验出的三等品更换为一等品或二等品；若不执行检验，则对卖出的每个三等品零件支付120元赔偿费用．现对一箱零件随机检验了10个，检出了1个三等品．将从两条生产线抽取的所有样本数据的频率视为概率，以整箱检验费用与赔偿费用之和的期望作为决策依据，是否需要对该箱余下的所有零件进行检验？请说明理由．

共享时间:2023-07-12 难度:1 相似度:1.5

解析

纠错

下载

组卷

dygzsxyn

2021-05-15

高中数学 | | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2021年陕西省西安中学高考数学六模试卷（理科）

更新:2021-05-15 08:47浏览量:17

普通登录

手机登录

微信扫码立即登录