服务热线
搜题▪组卷
如图所示，质量分别为mA=3kg、mB=2kg的物块A、B置于足够大的水平地面上，在大小F=25N的水平推力作用下，两物块一起由静止开始向右做匀加速直线运动，已知A、B与地面间的动摩擦因数分别为μA=0.5、μB=0.25，取重力加速度大小g=10m/s2。
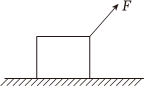如图所示，一个质量m=10kg的物体放在水平地面上。对物体施加一个与水平方向成37°的F=50N的拉力，使物体由静止开始运动。已知物体与水平面间的摩擦因数为0.2，求：
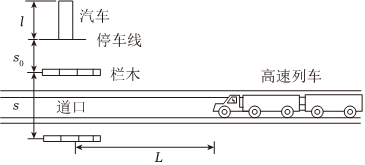
在一次救援中，一辆汽车停在一倾角为37°的小山坡坡底，突然司机发现在距坡底48m的山坡处一巨石以8m/s的初速度加速滚下，巨石和山坡间的动摩擦因数为0.5，巨石到达坡底后速率不变，在水平面的运动可以近似看成加速度大小为2m/s2的匀减速直线运动；司机发现险情后经过2s汽车才启动起来，并以0.5m/s2的加速度一直做匀加速直线运动（如图所示）．求：
连续刹车时，刹车片和刹车盘产生大量热量，温度升高很快，刹车效率迅速降低，容易造成刹车失灵．为了避免刹车失灵造成的危害，高速公路在一些连续下坡路段设置用砂石铺成的紧急避险车道，如图所示．现将某次汽车避险过程简化如下：一辆货车在倾角为30°的长直下坡路上以20m/s的速度匀速行驶，突然刹车失灵开始加速，此时汽车所受阻力为车重的0.4倍（发动机关闭），加速前进15s后冲上了倾角为53°的避险车道，在避险车道上运动17.5m后停下．将货车的加速、减速过程视为匀变速直线运动，求汽车：（sin53°=0.8，g=10m/s2）．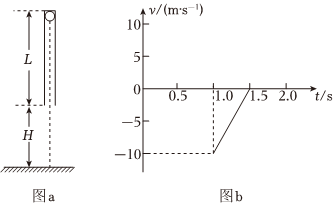
如图（a）所示，长为L的圆管竖直放置，质量M=4kg,顶端塞有质量为m=2kg的弹性小球（小球直径恰好等于圆管内径）。t=0时，让管从静止自由下落，t=1.0s时落地，落地后管立刻以与落地时大小相等的速率竖直弹起，第一次弹起后管上升过程的速度—时间图像如图（b）所示（以竖直向下为正方向），之后管每次落地后，总以与落地时相等的速率竖直弹起。已知小球始终没有从管中滑出，球与管之间的滑动摩擦力等于最大静摩擦力，不计空气阻力及圆管与地面碰撞的时间，重力加速度g取10m/s2，求：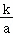
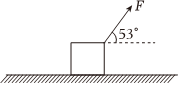，（取g＝10m/s2，sin37°＝
，cos37°＝），由于传送带速度不同，会导致物体从传送带底端运动至传送带顶端所用的时间有所变化．试表示此时间与传送带速度之间的函数关系．
如图所示，质量m=2kg的物体静止在水平地面上，现对物体施加一个大小F=10N，方向与水平方向成θ=53°的斜向上的拉力，使其沿水平地面向右做匀加速直线运动，经时间t=10s撤去推力F。已知物体与地面间的动摩擦因数为μ=0.25，sin53°=0.8，cos53°=0.6，g=10m/s2。求：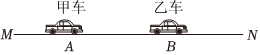
为了测定一辆电动汽车的加速性能，研究人员驾驶汽车沿平直公路从起点O处由静止启动，依次经过A、B、C三处标杆．已知A、B间的距离为L1，B、C间的距离为L2．测得汽车通过AB段与BC段所用的时间均为t,将汽车的运动过程视为匀加速行驶．求起点O与标杆A的距离．
ym@dyw.com
2024-02-27
高中物理 | 高一上 | 解答题
纠错
收藏
下载
相似
组卷
解析
