服务热线
搜题▪组卷
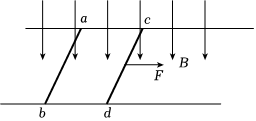 如图,电阻不计的两足够长的光滑平行金属导轨固定在绝缘水平面上,导轨间距为L=1m,导轨处于方向竖直向下的匀强磁场中,磁感应强度大小为B=1T。质量均为m=1kg、接入电路的有效电阻均为R=1Ω的金属棒ab、cd垂直于导轨放置,均处于静止状态。t=0时刻给cd棒一个方向水平向右、大小F=4N的拉力,t=4s时,金属棒ab和cd加速度刚好相等。此后撤去拉力F,整个过程棒与导轨接触良好。求:
如图,电阻不计的两足够长的光滑平行金属导轨固定在绝缘水平面上,导轨间距为L=1m,导轨处于方向竖直向下的匀强磁场中,磁感应强度大小为B=1T。质量均为m=1kg、接入电路的有效电阻均为R=1Ω的金属棒ab、cd垂直于导轨放置,均处于静止状态。t=0时刻给cd棒一个方向水平向右、大小F=4N的拉力,t=4s时,金属棒ab和cd加速度刚好相等。此后撤去拉力F,整个过程棒与导轨接触良好。求: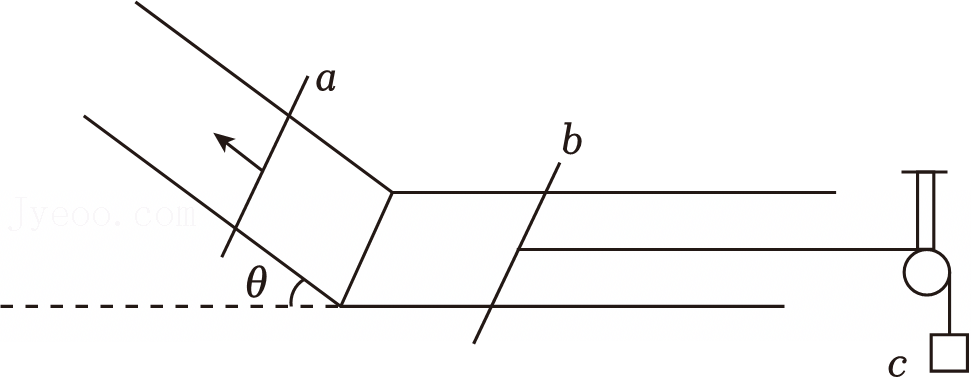
 如图所示,弯折成90°角的两根足够长金属导轨平行放置,形成左右两导轨平面,左导轨平面与水平面成α=53°,右导轨平面与水平面成θ=37°,两导轨相距L=0.2m,电阻不计。质量均为m=0.1kg、电阻均为R=0.1Ω、长度均为L=0.2m的金属棒ab、cd与导轨垂直接触形成闭合回路,金属杆与导轨间的动摩擦因数均为μ=0.5,整个装置处于方向平行于左导轨平面且垂直右导轨平面向上的匀强磁场中,磁感应强度B=0.5T。现让cd棒固定不动,将ab棒由静止释放,当ab棒沿导轨下滑x=6m时,速度刚好达到稳定。已知两杆下滑过程均保持与导轨垂直且接触良好,g取10m/s2,sin37°=0.6,cos37°=0.8。求:
如图所示,弯折成90°角的两根足够长金属导轨平行放置,形成左右两导轨平面,左导轨平面与水平面成α=53°,右导轨平面与水平面成θ=37°,两导轨相距L=0.2m,电阻不计。质量均为m=0.1kg、电阻均为R=0.1Ω、长度均为L=0.2m的金属棒ab、cd与导轨垂直接触形成闭合回路,金属杆与导轨间的动摩擦因数均为μ=0.5,整个装置处于方向平行于左导轨平面且垂直右导轨平面向上的匀强磁场中,磁感应强度B=0.5T。现让cd棒固定不动,将ab棒由静止释放,当ab棒沿导轨下滑x=6m时,速度刚好达到稳定。已知两杆下滑过程均保持与导轨垂直且接触良好,g取10m/s2,sin37°=0.6,cos37°=0.8。求: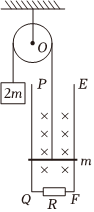 如图所示,在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电阻,导轨其余电阻不计。磁感应强度为B0的足够大的匀强磁场与导轨平垂直。其上方有一光滑的定滑轮,绕有轻质柔软不可伸长细线,线的一端系一质量为2m的重物,另一端系一质量为m、接入导轨间电阻为R的金属杆。开始时金属杆置于导轨下端QF处,由静止释放,当重物下降h时恰好达到稳定速度而匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,(忽略所有摩擦,重力加速度为g),求:
如图所示,在竖直平面内有间距为L的足够长的平行金属导轨PQ、EF,在QF之间连接有阻值为R的电阻,导轨其余电阻不计。磁感应强度为B0的足够大的匀强磁场与导轨平垂直。其上方有一光滑的定滑轮,绕有轻质柔软不可伸长细线,线的一端系一质量为2m的重物,另一端系一质量为m、接入导轨间电阻为R的金属杆。开始时金属杆置于导轨下端QF处,由静止释放,当重物下降h时恰好达到稳定速度而匀速下降。运动过程中金属杆始终与导轨垂直且接触良好,(忽略所有摩擦,重力加速度为g),求: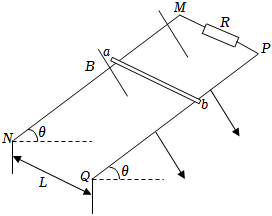 如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ=37°的绝缘斜面上,两导轨间距为L=0.5m,M、P两点间接有阻值为R=0.5Ω的电阻,一根质量为m=0.5kg的均匀直金属杆ab放在两导轨上,并与导轨垂直,金属杆的电阻为r=0.5Ω,整套装置处于磁感应强度为B=2T的匀强磁场中,磁场方向垂直于斜面向下,导轨电阻可忽略,让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦。(重力加速度g=10m/s2)
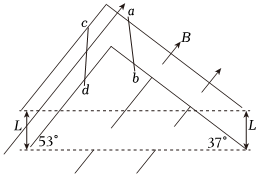
如图所示,两根足够长的直金属导轨MN、PQ平行放置在倾角为θ=37°的绝缘斜面上,两导轨间距为L=0.5m,M、P两点间接有阻值为R=0.5Ω的电阻,一根质量为m=0.5kg的均匀直金属杆ab放在两导轨上,并与导轨垂直,金属杆的电阻为r=0.5Ω,整套装置处于磁感应强度为B=2T的匀强磁场中,磁场方向垂直于斜面向下,导轨电阻可忽略,让ab杆沿导轨由静止开始下滑,导轨和金属杆接触良好,不计它们之间的摩擦。(重力加速度g=10m/s2)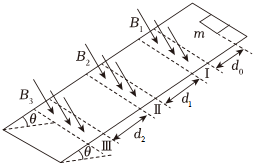 如图所示,足够长的斜面与水平面的夹角为θ=37°,空间中自上而下依次分布着垂直斜面向下的匀强磁场区域Ⅰ、Ⅱ、Ⅲ,磁场Ⅰ、Ⅱ间距d1为1.75m,磁场Ⅱ、Ⅲ间距d2为2.25m,一边长L=0.5m、质量m=1kg、电阻R=0.25Ω的正方形导线框放在斜面的顶端,导线框的下边距离磁场Ⅰ的上边界为d0=1.0m,导线框与斜面间的动摩擦因数μ=0.5。将导线框由静止释放,导线框匀速穿过每个磁场区域。重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8,求:
如图所示,足够长的斜面与水平面的夹角为θ=37°,空间中自上而下依次分布着垂直斜面向下的匀强磁场区域Ⅰ、Ⅱ、Ⅲ,磁场Ⅰ、Ⅱ间距d1为1.75m,磁场Ⅱ、Ⅲ间距d2为2.25m,一边长L=0.5m、质量m=1kg、电阻R=0.25Ω的正方形导线框放在斜面的顶端,导线框的下边距离磁场Ⅰ的上边界为d0=1.0m,导线框与斜面间的动摩擦因数μ=0.5。将导线框由静止释放,导线框匀速穿过每个磁场区域。重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8,求: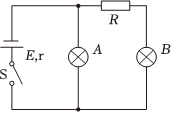 如图所示的闭合电路中,电源电动势E=6V,灯泡A标有“4.5V,3W”,灯泡B标有“3V,3W”。当开关S闭合时A、B两灯均 正常发光。求
如图所示的闭合电路中,电源电动势E=6V,灯泡A标有“4.5V,3W”,灯泡B标有“3V,3W”。当开关S闭合时A、B两灯均 正常发光。求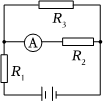 如图10所示的电路中,电阻R2=15Ω,R3=10Ω,电源的电动势E=12V,内电阻r=1Ω,安培表的读数I=0.4A.求:
如图10所示的电路中,电阻R2=15Ω,R3=10Ω,电源的电动势E=12V,内电阻r=1Ω,安培表的读数I=0.4A.求: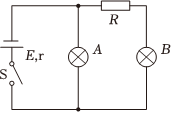 如图所示的闭合电路中,电源电动势E=6V,灯泡A标有“4.5V,3W”,灯泡B标有“3V,3W”。当开关S闭合时A、B两灯均 正常发光。求
如图所示的闭合电路中,电源电动势E=6V,灯泡A标有“4.5V,3W”,灯泡B标有“3V,3W”。当开关S闭合时A、B两灯均 正常发光。求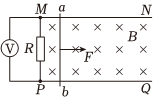 如图所示,光滑且足够长的金属导轨MN、PQ平行地固定在同一绝缘水平面上,导轨上停放一质量m=0.2kg的金属杆ab,两导轨间距L=0.2m,两导轨的左端接入电阻R=0.6Ω的定值电阻,位于两导轨之间的金属杆ab的电阻r=0.1Ω,导轨的电阻可忽略不计。整个装置处于磁感应强度大小B=0.5T的匀强磁场中,磁场方向竖直向下。现用一外力F水平向右拉金属杆ab,使之由静止开始向右做匀加速直线运动,在整个运动过程中金属杆ab始终与导轨垂直并接触良好,金属杆ab开始运动经t=10s时,定值电阻两端的电压U=1.2V,此时,求:
如图所示,光滑且足够长的金属导轨MN、PQ平行地固定在同一绝缘水平面上,导轨上停放一质量m=0.2kg的金属杆ab,两导轨间距L=0.2m,两导轨的左端接入电阻R=0.6Ω的定值电阻,位于两导轨之间的金属杆ab的电阻r=0.1Ω,导轨的电阻可忽略不计。整个装置处于磁感应强度大小B=0.5T的匀强磁场中,磁场方向竖直向下。现用一外力F水平向右拉金属杆ab,使之由静止开始向右做匀加速直线运动,在整个运动过程中金属杆ab始终与导轨垂直并接触良好,金属杆ab开始运动经t=10s时,定值电阻两端的电压U=1.2V,此时,求: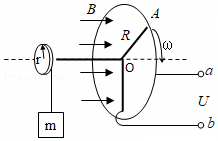
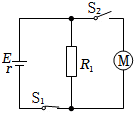 如图所示,电源的电动势E=110V,电阻R1=21Ω,电动机绕组的电阻R0=0.5Ω,电键S1始终闭合.当电键S2断开时,电阻R1的电功率是525W;当电键S2闭合时,电阻R1的电功率是336W,求:
如图所示,电源的电动势E=110V,电阻R1=21Ω,电动机绕组的电阻R0=0.5Ω,电键S1始终闭合.当电键S2断开时,电阻R1的电功率是525W;当电键S2闭合时,电阻R1的电功率是336W,求: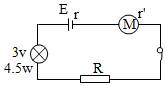 如图所示,已知电源电动势E=20V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 4.5W”的灯泡L和内阻r′=0.5Ω的小型直流电动机恰能正常工作,求:
如图所示,已知电源电动势E=20V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 4.5W”的灯泡L和内阻r′=0.5Ω的小型直流电动机恰能正常工作,求:
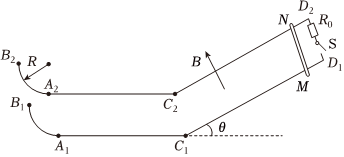 如图所示,倾角为θ=30°、宽度为d=1m、长为L=4m的光滑倾斜导轨,导轨C1D1、C2D2顶端接有定值电阻R0=15Ω,倾斜导轨置于垂直导轨平面斜向上的匀强磁场中,磁感应强度为B=5T,C1A1、C2A2是长为s=4.5m的粗糙水平轨道,A1B1、A2B2是半径为R=0.5m处于竖直平面内的1/4光滑圆环(其中B1、B2为弹性挡板),整个轨道对称。在导轨顶端垂直于导轨放一根质量为m=2kg、电阻不计的金属棒MN,当开关S闭合时,金属棒从倾斜轨道顶端静止释放,已知金属棒到达倾斜轨道底端前已达到最大速度,当金属棒刚滑到倾斜导轨底端时断开开关S,(不考虑金属棒MN经过C1、C2处和棒与B1、B2处弹性挡板碰撞时的机械能损失,整个运动过程中金属棒始终保持水平,水平导轨与金属棒MN之间的动摩擦因数为μ=0.1,g=10m/s2)。求:
如图所示,倾角为θ=30°、宽度为d=1m、长为L=4m的光滑倾斜导轨,导轨C1D1、C2D2顶端接有定值电阻R0=15Ω,倾斜导轨置于垂直导轨平面斜向上的匀强磁场中,磁感应强度为B=5T,C1A1、C2A2是长为s=4.5m的粗糙水平轨道,A1B1、A2B2是半径为R=0.5m处于竖直平面内的1/4光滑圆环(其中B1、B2为弹性挡板),整个轨道对称。在导轨顶端垂直于导轨放一根质量为m=2kg、电阻不计的金属棒MN,当开关S闭合时,金属棒从倾斜轨道顶端静止释放,已知金属棒到达倾斜轨道底端前已达到最大速度,当金属棒刚滑到倾斜导轨底端时断开开关S,(不考虑金属棒MN经过C1、C2处和棒与B1、B2处弹性挡板碰撞时的机械能损失,整个运动过程中金属棒始终保持水平,水平导轨与金属棒MN之间的动摩擦因数为μ=0.1,g=10m/s2)。求:
hen@dyw.com
2025-02-02
高中物理 | 高二上 | 计算题