如图所示足够长的斜面上有两辆小车车的质量为其尾部沿平行于斜面方向固定一轻弹簧与斜面间的最大静摩擦力与滑动摩擦力均为其中为斜面与水平方向夹角的正弦值为重力加速度的大小车的质量为与斜面光滑接触起初静止在斜面上某处将的前端轻触弹簧但不压缩弹簧由静止自由释放车已知当车开始运动时车的速度为证明车开始运动之后若的速度不会减为系统的动量守恒求此后的运动过程中弹簧长度最短时的速度和的最大速度重新

首页 > 试题列表 > 单题解析

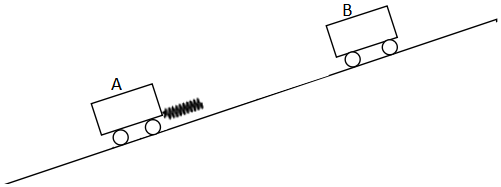151866. （2022•高新一中•三模） $德优题库$ 如图所示，足够长的斜面上有A、B两辆小车。A车的质量为m,其尾部沿平行于斜面方向固定一轻弹簧，A与斜面间的最大静摩擦力与滑动摩擦力均为3kmg,其中k为斜面与水平方向夹角的正弦值，g为重力加速度的大小。B车的质量为2m,与斜面光滑接触，起初，A静止在斜面上某处，将B的前端轻触弹簧，但不压缩弹簧，由静止自由释放B车。已知当A车开始运动时，B车的速度为v₀。
（1）证明：A车开始运动之后，若A的速度不会减为0，A、B系统的动量守恒。
（2）求此后的运动过程中弹簧长度最短时A的速度v₁和A的最大速度v₂。
（3）重新使A车静止在斜面上，将B车的前端置于弹簧原长处，释放B车的同时给B车沿斜面向下大小为

√

v₀的初速度。求B第一次离开弹簧时A、B的速度v_A、v_B。

共享时间:2022-04-05 难度:2

纠错

下载

相似

组卷

[考点]

常见力做功与相应的能量转化，动量守恒与能量守恒共同解决实际问题，

[答案]

（

）证明过程见解析。

（

）此后的运动过程中弹簧长度最短时

的速度

v₁

为

，

的最大速度

v₂

为

；

（

）

第一次离开弹簧时

、

的速度

v_A

、

v_B

分别为

2v₀

，

v₀

。

[解析]

解：（1）设斜面倾角为θ，已知k＝sinθ①，以A、B和弹簧组成的系统为研究对象，垂直斜面合力为零，
沿斜面方向合力为F_合＝3mgsinθ﹣3kmg②
①②结合得系统所受合力为零，故系统所受外力矢量和为零，因此：A车开始运动之后，若A的速度不会减为0，A、B系统的动量守恒。
（2）从A开始运动，到弹簧压缩最短过程中，A加速，B减速，最后两者速度相等，由系统动量守恒定律得2mv₀＝（m+2m）v₁
解得；
随后在弹力作用下，A继续加速，B继续减速，当弹簧弹力等于3kmg时，A达到最大速度，对A、B组成的系统从A开始运动到速度最大过程中，
根据动量守恒定律得2mv₀＝mv₂+2mv′_B③
因为此过程初始时弹簧弹力也是3kmg，故A、B下降的高度相等设为h，由功能关系得④
联立①③④代入数据解得v₂＝0（舍去），；
（3）从释放B车的同时给B车沿斜面向下大小为v₀的初速度到A开始运动之前，由功能关系得⑤
已知由静止释放B到A开始运动时，B车的速度为v₀，B经历同一过程，合力做功相同，则

⑥
联立⑤⑥解得v＝2v₀
A开始以2v₀运动后到停止运动前，A、B组成的系统动量守恒，在弹簧恢复原长时，B第一次离开弹簧，根据动量守恒定律得
2m（2v₀）＝mv_A+2mv_B⑦
从释放B开始以v₀的初速度运动到第一次脱离弹簧，由题意可知，两者下降的高度相等，设为h′，根据功能关系得⑧
联立①⑦⑧得，，解一元二次方程得，v_B＝v₀，v_A＝2v₀；，，根据题意可知当B第一次离开弹簧前，v_A＞v_B，故第二组解舍去，
即B第一次离开弹簧时A、B的速度分别为v_A＝2v₀，v_B＝v₀。
答：（1）证明过程见解析。
（2）此后的运动过程中弹簧长度最短时A的速度v₁为，A的最大速度v₂为；
（3）B第一次离开弹簧时A、B的速度v_A、v_B分别为2v₀，v₀。

[点评]

本题考查了"常见力做功与相应的能量转化，动量守恒与能量守恒共同解决实际问题，"，属于"易错题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

159789. （2022•周至四中•高二下二月）在列车编组站里，一辆M₁=1.8×10⁴kg的货车在平直轨道是以V₁=2m/s的速度运动，碰上一辆M₁=2.2×10⁴kg的静止的货车，它们碰撞后结合在一起继续运动．求货车碰撞后的速度．

共享时间:2022-06-26 难度:1 相似度:1.5

解析

纠错

下载

组卷

159130. （2023•高新一中•高二上一月）如图所示，一沙袋用无弹性轻细绳悬于O点。开始时沙袋处于静止，此后弹丸以水平速度击中沙袋后均未穿出。第一次弹丸的速度为v₁，打入沙袋后二者共同摆动的最大摆角为30°。当他们第1次返回图示位置时，第2粒弹丸以水平速度又击中沙袋，使沙袋向右摆动且最大摆角仍为30°。若弹丸质量是沙袋质量的

倍，求v₁：v₂的比值是多少？

共享时间:2023-10-14 难度:2 相似度:1

解析

纠错

下载

组卷

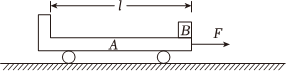160844. （2015•西安中学•五模） $德优题库$ 如图所示，水平地面上静止放置一辆小车A，质量m_A=4kg,上表面光滑，小车与地面间的摩擦力极小，可以忽略不计，可视为质点的物块B置于A的最右端，B的质量m_B=2kg,现对A施加一个水平向右的恒力F=10N，A运动一段时间后，小车左端固定的挡板与B发生碰撞，碰撞时间极短，碰后A、B粘合在一起，共同在F的作用下继续运动，碰撞后经时间t=0.6s,二者的速度达到v_t=2m/s,求
（1）A开始运动时加速度a的大小；
（2）A、B碰撞后瞬间的共同速度v的大小；
（3）A的上表面长度l。

共享时间:2015-05-09 难度:2 相似度:1

解析

纠错

下载

组卷

151819. （2015•西安中学•七模）如图所示，一质量为m＝2kg的滑块从半径为R＝0.2m的光滑四分之一圆弧轨道的顶端A处由静止滑下，A点和圆弧对应的圆心O点等高，圆弧的底端B与水平传送带平滑相接。已知传送带匀速运行速度为v₀＝4m/s，B点到传送带右端C点的距离为L＝2m。当滑块滑到传送带的右端C时，其速度恰好与传送带的速度相同。（g＝10m/s²）求：
（1）滑块到达底端B时对轨道的压力；
（2）滑块与传送带间的动摩擦因数μ；
（3）此过程中，由于滑块与传送带之间的摩擦而产生的热量Q。

共享时间:2015-06-09 难度:3 相似度:0.83

解析

纠错

下载

组卷

158282. （2022•西安中学•二模）某游戏装置可以简化为如图所示：游客乘坐滑椅（可视为质点）从固定光滑圆弧轨道上的B点处无初速滑下后冲上静止在光滑水平面上的滑板A。已知游客与滑椅的质量为m，滑板A的质量为2m，滑椅与滑板间的动摩擦因数为μ，滑板A足够长，滑椅不会从滑板表面滑出，圆弧轨道的半径为R，O点为圆弧轨道的圆心，θ＝60°，重力加速度为g，求：
（1）滑椅滑到圆弧轨道最低点时对轨道的压力大小；
（2）滑椅滑上A后经多长时间不再相对A滑动；
（3）若滑块A至少多长才能满足要求。