服务热线
搜题▪组卷
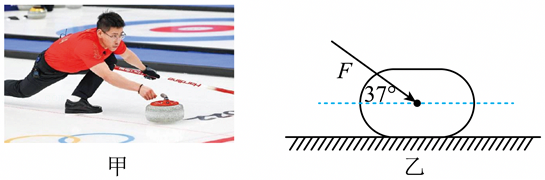
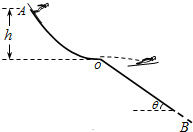 如图所示,在冬奥会上,跳台滑雪运动员从滑道上的A点由静止滑下,经时间t0从跳台末端的O点沿水平方向飞出.O点又是斜坡OB的起点,A点与O点在竖直方向的高度差为h,斜坡OB的倾角为θ.运动员的质量为m,重力加速度为g.不计一切摩擦和空气阻力.求:
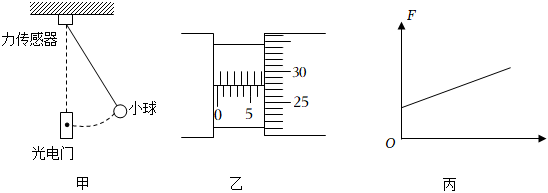
如图所示,在冬奥会上,跳台滑雪运动员从滑道上的A点由静止滑下,经时间t0从跳台末端的O点沿水平方向飞出.O点又是斜坡OB的起点,A点与O点在竖直方向的高度差为h,斜坡OB的倾角为θ.运动员的质量为m,重力加速度为g.不计一切摩擦和空气阻力.求: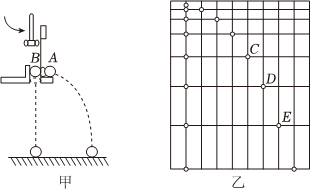 一同学利用实验室设备配合频闪摄像机设计了如下实验来探究“平抛运动的规律”。实验步骤如下:
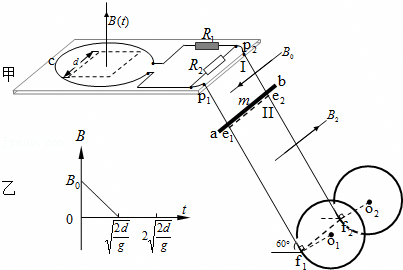
一同学利用实验室设备配合频闪摄像机设计了如下实验来探究“平抛运动的规律”。实验步骤如下: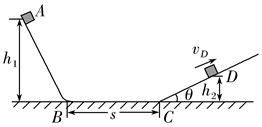 如图所示装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接,其中轨道AB、CD段是光滑的,水平轨道BC的长度s=5m,轨道CD足够长且倾角θ=37°,A、D两点离轨道BC的高度分别为h1=4.30m、h2=1.35m。现让质量为m的小滑块自A点由静止释放。已知小滑块与轨道BC间的动摩擦因数μ=0.5,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8
如图所示装置由AB、BC、CD三段轨道组成,轨道交接处均由很小的圆弧平滑连接,其中轨道AB、CD段是光滑的,水平轨道BC的长度s=5m,轨道CD足够长且倾角θ=37°,A、D两点离轨道BC的高度分别为h1=4.30m、h2=1.35m。现让质量为m的小滑块自A点由静止释放。已知小滑块与轨道BC间的动摩擦因数μ=0.5,取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8

A.小球下落过程中重力做功为100J
B.小球落地时重力的瞬时功率为100W
C.小球落地时的速度大小是15m/s
D.小球落地时的速度方向与水平地面成45°角
A.物体重力做的功为mgh
B.物体克服阻力做功为![]()
C.物体重力势能增加了mgh
D..物体动能增加![]()

dygzwlgr
2015-04-08
高中物理 | | 实验题