如图所示在一个圆形区域内两个方向相反且都垂直于纸面的匀强磁场分布在以直径为边界的两个半圆形区域中直径与的夹角为一质量为带电荷量为的粒子以某一速度从区的边缘点处沿与成角的方向射入磁场随后该粒子以垂直于的方向经过圆心进入区最后再从处射出磁场已知该粒子从射入到射出磁场所用的时间为忽略粒子重力求画出粒子在磁场和中的运动轨迹粒子在磁场和中的轨道半径和比值区和区中磁感应强

首页 > 试题列表 > 单题解析

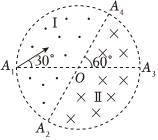151732. （2015•西安八十三中•二模） $德优题库$ 如图所示，在一个圆形区域内，两个方向相反且都垂直于纸面的匀强磁场分布在以直径A₂A₄为边界的两个半圆形区域Ⅰ、Ⅱ中，直径A₂A₄与A₁A₃的夹角为60°，一质量为m、带电荷量为+q的粒子以某一速度从Ⅰ区的边缘点A₁处沿与A₁A₃成30°角的方向射入磁场，随后该粒子以垂直于A₂A₄的方向经过圆心O进入Ⅱ区，最后再从A₄处射出磁场．已知该粒子从射入到射出磁场所用的时间为t,（忽略粒子重力），求：
（1）画出粒子在磁场Ⅰ和Ⅱ中的运动轨迹；
（2）粒子在磁场Ⅰ和Ⅱ中的轨道半径r₁和r₂比值；
（3）Ⅰ区和Ⅱ区中磁感应强度的大小B₁和B₂．

共享时间:2015-03-21 难度:3

纠错

下载

相似

组卷

[考点]

牛顿第二定律的简单应用，牛顿第二定律与向心力结合解决问题，带电粒子在匀强磁场中的圆周运动，

[答案]

见试题解答内容

[解析]

解：（1）设粒子的入射速度为v，已知粒子带正电，故它在磁场中先顺时针做圆周运动，再逆时针做圆周运动，最后从A₄点射出，运动轨迹如图所示，
（2）用B₁、B₂、R₁、R₂、T₁、T₂分别表示在磁场Ⅰ区Ⅱ磁感应强度、轨道半径和周期
qvB₁＝m…①
qvB₂＝m…②
T₁＝…③
T₂＝…④
设圆形区域的半径为r，如答图5所示，已知带电粒子过圆心且垂直A₃A₄进入Ⅱ区磁场，
连接A₁A₂，ΔA₁OA₂为等边三角形，A₂为带电粒子在Ⅱ区磁场中运动轨迹的圆心，
其半径R₁＝A₁A₂＝OA₂＝r…⑤
圆心角∠A₁A₂O＝60°，带电粒子在Ⅰ区磁场中运动的时间为：t₁＝T₁…⑥
带电粒子在Ⅱ区磁场中运动轨迹的圆心在OA₄的中点，即R＝r…⑦
（3）在Ⅱ区磁场中运动时间为t₂＝T₂…⑧
带电粒子从射入到射出磁场所用的总时间t＝t₁+t₂…⑨
由以上各式可得：B₁＝…⑩
B₂＝
故I区磁感应强度为，II区磁感应强度为：．
答：（1）画出粒子在磁场I和II中的运动轨迹如上图；
（2）粒子在磁场I和II中的轨道半径r₁和r₂比值为2：1；
（3）I区和II区中磁感应强度的大小分别为和．

[点评]

本题考查了"牛顿第二定律的简单应用，牛顿第二定律与向心力结合解决问题，带电粒子在匀强磁场中的圆周运动，"，属于"典型题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

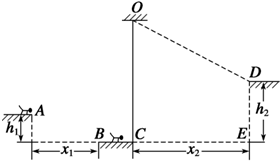151733. （2015•西安八十三中•二模） $德优题库$ 山谷中有三块大石头和一根不可伸长的轻质青藤，其示意图如图所示。图中A、B、C、D均为石头的边缘点，O为青藤的固定点，h₁=1.8m,h₂=4.0m,x₁=4.8m,x₂=8.0m。开始时，质量分别为M=10kg和m=2kg的大、小两只滇金丝猴分别位于左边和中间的石头上，当大猴发现小猴将受到伤害时，迅速从左边石头A点以水平速度跳下，跳到中间石头，大猴抱起小猴跑到C点，抓住青藤的下端荡到右边石头的D点，此时速度恰好为零。运动过程中猴子均看成质点，空气阻力不计，重力加速度g=10m/s²，求：
（1）大猴子从A点水平跳离时速度的最小值；
（2）猴子刚抓住青藤荡起时的速度大小；
（3）猴子刚抓住青藤荡起时，青藤对猴子的拉力大小。

共享时间:2015-03-21 难度:3 相似度:1.34

解析

纠错

下载

组卷

dygzwlgr

2015-03-21

高中物理 | | 探究题

下载量
浏览量
收益额

相关试卷 更多>>

2015年陕西省西安市八十三中物理二模试卷

更新:2015-03-21 09:03浏览量:30

普通登录

手机登录

微信扫码立即登录