如图中则的最小整数值为如图中点为边的中点过作分别交边于请求出长度的最小值如图有一块四边形草地规划部门计划在这块空地内种植花卉计划在边上分别取点利用小路把这块草地分割开在四边形内种植郁金香其他区域种植草坪为观赏长廊已知

首页 > 试题列表 > 单题解析

274229. （2024•高新一中•七模）（1）如图1，△ABC中，AB＝AC＝a，BC＝8，则a的最小整数值为　5　．
（2）如图2，△ABC中，∠C＝90°，BC＝3，AC＝4，点O为AB边的中点，过O作OE⊥OF，OE、OF分别交边BC、AC于E、F，请求出EF长度的最小值．
（3）如图3，有一块四边形草地ABCD，规划部门计划在这块空地内种植花卉，计划在边BC、CD上分别取点E、F，利用小路AE、AF把这块草地分割开，在四边形AECF内种植郁金香，其他区域种植草坪，EF为观赏长廊．已知AD∥BC，

，AD＝100m，BC＝140m，∠B＝45°．设计师认为当tan∠EAF＝2时，规划更美观，已知种植郁金香每平米20元，请帮助规划部门解决问题：当观赏长廊EF长度最小时，求出种植郁金香所需费用（观赏长廊所占面积忽略不计）．

共享时间:2024-06-01 难度:1

纠错

下载

相似

组卷白板

[考点]

四边形综合题，

[校正]

[答案]

（1）5．
（2）EF长度的最小值为

；（3）当观赏长廊EF长度最小为40

m时，种植郁金香所需费用为88000元．

[解析]

解：（1）∵AB+AC＞BC，
∴a+a＞8，
∴a＞4，
∴a的最小整数值为5，
故答案为：5．
（2）如图2，取EF中点M，连接CM、OM、CO，

∵∠C＝90°，OE⊥OF，
∴CM＝

EF，OM＝

EF，
∴EF＝CM+OM，
∵CM+OM≥OC，
∴EF≥OC，
在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，
∴AB＝

＝

＝5，
∵点O为AB边的中点，
∴OC＝

AB＝

，
∴EF≥

，
故EF长度的最小值为

．
（3）如图3，连接AC，过点A作AG⊥BC于G，过点C作CH⊥AD于H，

∵AD∥BC，
∴∠AGC＝∠GAH＝∠AHC＝90°，
∴四边形AGCH是矩形，
在Rt△ABG中，∠B＝45°，AB＝80

m，
∴BG＝AG＝

AB＝

×80

＝80（m），
∴GC＝BC﹣BG＝140﹣80＝60（m），CH＝AG＝80m，
∴AH＝GC＝60m，
∴DH＝AD﹣AH＝100﹣60＝40（m），
在Rt△ACG中，AC＝

＝

＝100（m），
∵tan∠EAF＝2，tan∠D＝

＝

＝2，
∴tan∠EAF＝tan∠D，
∴∠EAF＝∠D，
∵AD∥BC，
∴∠D+∠BCD＝180°，
∴∠EAF+∠BCD＝180°，
∴四边形AECF是圆内接四边形，
设AC中点为K，过点K作直线l⊥AC于K，则圆心O肯定在直线l上，如图4，连接OA、OE、OF，过点O作OM⊥EF于M，

设⊙O的半径为rm，则OA＝OE＝OF＝rm，
∵OA≥AK，
∴r≥50m，
∵

＝

，
∴∠EAF＝

∠EOF，
∵OM⊥EF，
∴EM＝MF，
∵OE＝OF，
∴∠EOM＝∠FOM＝

∠EOF，
∴∠EAF＝∠EOM＝∠FOM，
∴tan∠EAF＝tan∠FOM＝

＝2，
∴OM＝

FM，
在Rt△FOM中，OM²+FM²＝OF²，
∴（

FM）²+FM²＝r²，
∴FM＝

r，
∴EF＝2FM＝

r，
∵r≥50，
∴当r＝50时，EF取得最小值，最小值为40

，此时，圆心O与点K重合，AC为⊙O的直径，
∴∠AEC＝∠AFC＝90°，AE＝AG＝80m，CE＝CG＝60m，
∴S_△AEC＝

AE•CE＝

×80×60＝2400（m²），
在Rt△ADF中，tan∠D＝

＝2，AD＝100m，
∴AF＝2DF，
∵AF²+DF²＝AD²，
∴（2DF）²+DF²＝100²，
∴DF＝20

m，AF＝40

m，
∵AC＝AD＝100m，AF⊥CD，
∴CF＝DF＝20

m，
∴S_△AFC＝

AF•CF＝

×40

×20

＝2000（m²），
∴S_{四边形AECF}＝S_△AEC+S_△AFC＝2400+2000＝4400（m²），
∴4400×20＝88000（元），
故当观赏长廊EF长度最小为40

m时，种植郁金香所需费用为88000元．

[点评]

本题考查了"四边形综合题，"，属于"常考题"，熟悉题型是解题的关键。

转载声明：

本题解析属于发布者收集录入，如涉及版权请向平台申诉！！版权申诉

考点说明

灰色代表去掉的考点，绿色代表未变动的考点，红色代表新增的考点

相似题 全部同步专题复习模拟真题联考专练月考周考期中期末单元寒假暑假副题

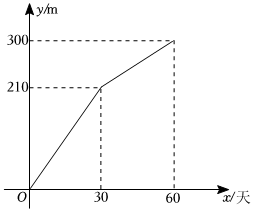196609. （2024•西工大附中•七下期末） $德优题库$ 甲、乙两个工程组同时挖掘某段隧道，两组每天挖掘长度均保持不变，合作一段时间后，乙组因维修设备而停工，甲组单独完成了剩下的任务，甲、乙两组挖掘的长度之和y（m）与甲组挖掘时间x（天）之间的关系如图所示．
（1）甲组比乙组多挖掘了天，甲组挖掘的总长度是 m；
（2）求乙组停工后y关于x的关系式．

共享时间:2024-07-17 难度:1 相似度:2

解析

纠错

下载

组卷白板

274305. （2024•高新一中•九模）问题提出
（1）如图①，在边长为10的菱形ABCD中，点E为AB上一点，AE=3，在CD边上有一点F，连接EF，若EF平分菱形ABCD的面积，则DF的长为；
问题探究
（2）如图②，在Rt△ABC中，∠C=90°，M，N分别是BC，AC上的动点，且MN=2，点P是MN的中点，若AC=3，BC=4，请求出点P到AB距离的最小值；
问题解决
（3）如图③，某公园计划建一个形状为▱ABCD的游乐场，其中CD=90米，BC=150米，连接AC，AC⊥AB．为方便工作人员通过，要留出一条快速通道EF，E、F是▱ABCD边上的动点（可与顶点重合）．根据设计要求，线段EF平分▱ABCD的面积，过点C作CP⊥EF于点P，要将△ADP区域修建为家长休息等待区，为使游乐场容纳更多的游乐设施，要求家长休息等待区（即△ADP）的面积尽可能地小，问△ADP的面积是否存在最小值？若存在，请求出△ADP的面积最小值及此时快速通道EF的长度；若不存在，请说明理由．

$德优题库$

共享时间:2024-06-15 难度:1 相似度:2

解析

纠错

下载

组卷白板

882. （2013•陕西省•真题）问题探究：
（1）请在图①中作出两条直线，使它们将圆面四等分；
（2）如图②，M是正方形ABCD内一定点，请在图②中作出两条直线（要求其中一条直线必须过点M）使它们将正方形ABCD的面积四等分，并说明理由．
问题解决：
（3）如图③，在四边形ABCD中，AB∥CD，AB+CD=BC，点P是AD的中点，如果AB=a，CD=b，且b＞a，那么在边BC上是否存在一点Q，使PQ所在直线将四边形ABCD的面积分成相等的两部分？如若存在，求出BQ的长；若不存在，说明理由．

共享时间:2013-11-18 难度:3 相似度:2

解析

纠错

下载

组卷白板

1052. （2019•陕西省•真题）问题提出：
（1）如图1，已知△ABC，试确定一点D，使得以A，B，C，D为顶点的四边形为平行四边形，请画出这个平行四边形；
问题探究：
（2）如图2，在矩形ABCD中，AB＝4，BC＝10，若要在该矩形中作出一个面积最大的△BPC，且使∠BPC＝90°，求满足条件的点P到点A的距离；
问题解决：
（3）如图3，有一座塔A，按规定，要以塔A为对称中心，建一个面积尽可能大的形状为平行四边形的景区BCDE．根据实际情况，要求顶点B是定点，点B到塔A的距离为50米，∠CBE＝120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由．（塔A的占地面积忽略不计）

共享时间:2019-07-05 难度:5 相似度:2

解析

纠错

下载

组卷白板

285701. （2022•滨河中学•五模）如图，以△ABC的边AC为直径的⊙O恰好为△ABC的外接圆，∠ABC的平分线交⊙O于点D，过点D作DE∥AC交BC的延长线于点E．
（1）求证：DE是⊙O的切线；
（2）若AB＝8，tan∠BAC＝

，求DE的长．

共享时间:2022-05-14 难度:1 相似度:2

解析

纠错

下载

组卷白板

27864. （2024•爱知中学•九上期末）【问题探究】
（1）如图1，在矩形ABCD中，AB=4，点E、F分别为边AD、BC上的点，且AE=1，BF=2，P为边AB上一动点，连接EP、PF，则EP+PF的最小值为．
（2）如图2，在矩形ABCD中，AB=4，BC=8，点E、F分别在边AD和BC上，连接AC，EF⊥AC于M，求EF的长．
【问题解决】
（3）某市进行绿化改造，美化生态环境．如图3，将一块四边形的空地ABCD改造成了供市民休闲锻炼的公园．已知：在四边形ABCD中，AB∥CD，∠C=90°，tan∠CDA=2，BC=60米，AB=110米，在公园的AD边上有一个出口M，经测量MD=2MA，为了方便市民，现计划在公园的AB边和CD边上分别建一个休息亭F和E，然后铺设观景道BE、EF、FM，并且EF⊥BM，若要使这三条观景道的距离和最小（即BE+EF+FM最小），请求出休息亭F距离点A多远？并求出BE+EF+FM的最小值．（小路面积忽略不计，结果保留根号）
$德优题库$

共享时间:2024-02-17 难度:1 相似度:2

解析

纠错

下载

组卷白板

61343. （2023•爱知中学•九上期末）（1）如图1，AD∥BC，连接AB、AC、BD、CD，则S_△ABC S_△BCD．
（2）如图2，在△ABC中，∠BAC=45°，BC=6，求△ABC的最大面积．
（3）如图3，西安市规划局计划打造一片公共休闲区域（即四边形ABCD），准备在△ABC中种植绿植，同时以AC为边在它的左侧打造一个等边三角形的花卉园（即△ACD），要求∠A=60°，BC=600m,且使四边形ABCD的面积最大，请问是否存在满足要求的四边形ABCD，如果存在，求出四边形ABCD面积的最大值，如果不存在，请说明理由．
$德优题库$

共享时间:2023-03-02 难度:1 相似度:2

解析

纠错

下载

组卷白板

61390. （2023•爱知中学•七上期末）如图，已知△ABC中，∠B=90°，将△ABC沿着射线BC方向平移得到△DEF，其中点A、点B、点C的对应点分别是点D、点E、点F，且CE=DE．
$德优题库$
（1）如图①，如果AB=6，BC=3，那么平移的距离等于；（请直接写出答案）
（2）如图②，将△DEF绕着点E逆时针旋转90°得到△CEG，连接AG，如果AB=a,BC=b,求△ACG的面积；
（3）如图③，在（2）题的条件下，分别以AB，BC为边向外作正方形，正方形的面积分别记为S₁，S₂，且满足S₁-S₂=16，如果平移的距离等于8，求出△ACG的面积．

共享时间:2023-02-15 难度:1 相似度:2

解析

纠错

下载

组卷白板

173820. （2024•高新一中•九上三月）问题提出：
（1）如图①，在▱ABCD中，∠A＝60°，AB＝8，AD＝6，点E在AD上，且AE＝4，点F是CD的中点，求四边形BCFE的面积．（结果保留根号）
问题解决：
（2）某地进行河滩治理，美化人居生态环境．如图②所示，现规划在河畔的一处滩地上建一个五边形河畔公园ABCDE．按设计要求，要在五边形河畔公园ABCDE内挖一个四边形人工湖OPMN，使点O、P、M、N分别在边AB、BC、CD、AE上，且满足BO＝2AN＝2CP，AO＝CM．已知五边形ABCDE中，∠A＝∠B＝∠C＝90°，AB＝1800m，BC＝1200m，AE＝900m，CD＝1300m．为满足人工湖周边各功能场所及绿化用地需要，想让人工湖OPMN的面积尽可能小．请问，是否存在符合设计要求的面积最小的四边形人工湖OPMN？若存在，求出四边形OPMN面积的最小值以及这时点N到点A的距离；若不存在，请说明理由．

共享时间:2024-01-25 难度:1 相似度:2

解析

纠错

下载

组卷白板

185129. （2025•铁一中学•八下期中）（1）阅读材料：如图①，在Rt△ABC中，∠ACB=90°，AC=2，∠ABC=30°，△ACE是等边三角形，M为△ABC内任意一点，连接CM，将CM绕点C逆时针旋转60°得到CN，连接EN、AM、BM．
①△CMN的形状是；
②AM+BM+CM是否存在最小值，若存在，求出这个最小值，若不存在，请说明理由；
（2）如图②，城市规划部门准备在一块边长40米的正方形空地ABCD建设口袋公园，四个顶点A、B、C、D为公园入口，公园内有两个凉亭E、F，为方便市民散步，需修建健身步道连接AE、BE、EF、DF、CF．为节约建设成本，应将E、F修建在何处可使修建步道之和最短？最短距离为多少？
$德优题库$

共享时间:2025-05-10 难度:1 相似度:2

解析

纠错

下载

组卷白板

190494. （2025•碑林区•九上期末）【问题提出】
（1）如图1，AD与BE相交于点C，连接AB，DE，∠A＝∠E，

，若AB的长为21，求DE的长；
【问题解决】
（2）如图2，四边形ABCD是一个植物园的花卉区，经测量，AB＝BC＝CD＝AD，工作人员计划将该花卉区进行扩建，在对角线AC上取一点E，在边BC的延长线上取一点F，连接BE，EF，DF，EF与CD交于点G，根据工作人员的规划要求，BE与EF相等，EF与CD互相垂直，在扩建部分（△CDF区域内）新增加一种花卉，请你判断∠CDF与∠ADC之间的数量关系，并说明理由．

共享时间:2025-02-05 难度:1 相似度:2

解析

纠错

下载

组卷白板

192152. （2024•高新一中•八下一月）【问题出示】
（1）如图①，等腰△ABC中，∠BAC=30°，BC=BA=16，点M是直线AC上的动点，线段BM的最小值是．
$德优题库$
【问题探究】
（2）如图②，线段BM最短时，在（1）的条件下，线段BN是△ABM的角平分线，点P、Q分别在边BN、BM上运动，连接MP、QP，MP+QP的最小值是
【问题拓展】
（3）如图③，线段BM最短时，在（1）的条件下，点E在边CM上运动，连接BE，将线段BE绕点B顺时针旋转60°，得到线段BF，连接MF，求线段MF的最小值．
【问题解决】
按照住建部制定的楼间距国家标准，南北朝向的小区，各栋楼之间的距离不小于前排楼高的0.7倍，例如：前排房屋的楼高是20米，那么后排房屋与前排房屋的距离至少要14米才符合要求．
（4）如图④，是某居民小区的部分平面示意图，四边形ABCD各边长都为90米，且两组对边分别平行，∠B=120°，DE长30米，AB边上任意一点F，计划在线段EF、FG、DG上修建三条小路，点G处修建业主活动楼，其中EF=FG，且∠EFG=60°．小区最南边一排（即线段AD处）楼高70米，当线段DG取最小值时，点G处的业主活动楼到线段AD处楼房的距离是否符合楼间距标准？请说明理由．

共享时间:2024-04-21 难度:1 相似度:2

解析

纠错

下载

组卷白板

210630. （2025•师大附中•六模）折纸是我国传统的民间艺术，通过折纸不仅可以得到许多美丽的图形，折纸的过程还蕴含着丰富的数学知识，在综合与实践课上，老师让同学们准备了一张边长为6cm的正方形纸片，以“正方形的折叠”为主题开展了数学探究活动．
【操作判断】
操作一：如图①，在正方形ABCD的边AD上任选一点E，沿BE折叠，使点A落在点G处，把纸片展平，折痕BE与对角线AC交于点I；
操作二：将边BC折叠，使点C落在射线BG上，折痕交CD于点F，把纸片展平，折痕BF与正方形的对角线AC交于点H．
$德优题库$
（1）根据以上操作，得∠EBF的度数为．
【迁移探究】
（2）经过多次操作，同学们发现EF与HI的比值不变，试求出该比值．
【拓展提升】
（3）小明在操作中不慎将正方形纸片撕破，得到一个矩形ABCD，其中AB为6cm,AD为4cm,如图②，经过上述操作一、二，得到折痕BE、BF，EG的延长线与BF的延长线交于点K，当点E在线段AD（E不与A重合）上运动时，求点K到直线AD的最大距离．

共享时间:2025-05-30 难度:1 相似度:2

解析

纠错

下载

组卷白板

211020. （2025•高新一中•七模）【问题提出】
如图①，在Rt△ABC中，∠B=90°，AB=BC=4，E是AB边上的中点，点P，Q分别是BC，AC上的动点，则EP+PQ的最小值是；
【问题解决】
如图②，某大型工厂生产区域内，有一个矩形场地ABCD，其中点D为原材料入口，修建在DC段的点G为成品出口．在生产区域内，有两处重要的生产加工点E和F，分别位于场地的DA，DB段，并且DE=DF．为了实现从生产加工点到成品出口的高效运输（即成品从生产加工点经质检区域输送到出口的过程更为高效），工厂规划修建一个调度中心P与一处位于BC段的半圆形自动化质检区域（圆心为O）．该调度中心需同时满足以下两个条件：①使P到生产加工点E，F的距离相等，即PE=PF；②使运输线路PM+NG的长度最短（其中M，N为半圆质检区域O上的任意两点）．已知AD=300米，AB=400米，CG=100米，质检区域半径r=20米．请问是否存在符合要求的调度中心点P，若存在，求出PM+NG的最小值和此时OC的距离；若不存在，请说明理由．
$德优题库$

共享时间:2025-06-08 难度:1 相似度:2

解析

纠错

下载

组卷白板

212450. （2025•交大附中•三模） “综合与实践”课上，同学们通过剪拼图形，用数学的眼光看问题，感受图形的变换美！
【特例感知】
（1）如图1，纸片ABCD为矩形，且AD＝20厘米，AB＝10厘米，点E，F分别为边AD，BC的中点，沿EF将纸片剪成两部分，将纸片DEFC沿纸片ABFE的对角线EB方向向上平移．
①当纸片DEFC平移至点E′与EB的中点O重合时，两个纸片重叠部分FGE′H的面积与原矩形纸片ABCD的面积之比是　　．
②当两个纸片重叠部分FGE′H的面积与原矩形纸片ABCD的面积之比是

时，则平移距离EE′为　　．
【类比探究】
（2）如图2，当纸片KLMN为菱形，KN＝a（a＞2），∠N＝60°时，将纸片KLMN沿其对角线KM剪开，将纸片KLM沿KM方向向上平移．当两个纸片重叠部分K′PM的面积与纸片KLM的面积之比为

时，求平移距离KK′（用含a的式子表示）．
【拓展延伸】
（3）如图3，在直角三角形纸片△ABC中，∠C＝90°，AC＝18厘米，BC＝24厘米，取AB，BC中点D，E，将△ABC沿DE剪开，得到四边形ACED和△DEB，将△DEB绕点D顺时针旋转得到△DFG．在△DFG旋转一周的过程中，求△CFG面积的最大值．

共享时间:2025-04-13 难度:1 相似度:2

解析

纠错

下载

组卷白板

csyn@dyw.com

2024-06-01

初中数学 | | 解答题

下载量
浏览量
收益额

相关试卷 更多>>

2024年陕西省西安市雁塔区高新一中中考数学七模试卷

更新:2024-06-01 10:37浏览量:45

微信扫码立即登录

AI助手

登录

注册

微信扫码立即登录

AI助手