服务热线
搜题▪组卷
的中点，桥下水面的宽度AB=24m,点P到水面AB的距离PH=8m.点P1，P2均在上，
=
，且P1P2=10m,在点P1，P2处各装有一个照明灯，图中△P1CD和△P2EF分别是这两个灯的光照范围．两灯可以分别绕点P1，P2左右转动，且光束始终照在水面AB上．即∠CP1D，∠EP2F可分别绕点P1，P2按顺（逆）时针方向旋转（照明灯的大小忽略不计），线段CD，EF在AB上，此时，线段ED是这两灯照在水面AB上的重叠部分的水面宽度．已知∠CP1D=∠EP2F=90°，在这两个灯的照射下，当整个水面AB都被灯光照到时，求这两个灯照在水面AB上的重叠部分的水面宽度．（可利用备用图解答）
OP=2，
x,GF=
x,x,
=
=
=
，
=
，
；
的中点，PH⊥AB，AB=12m,
=
=
=12（m），
=
=
（m），
=
，
=
，
，， +-24=
（m）；m；m.
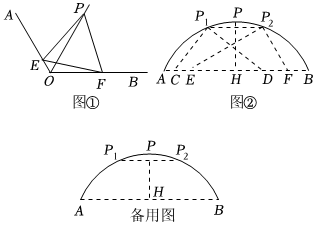
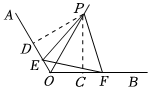
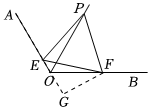
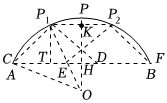
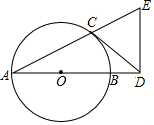如图，AB是⊙O的直径，点C是⊙O上一点，过点C作⊙O的切线交AB的延长线于点D，过点D作DE⊥AD交AC的延长线于点E．
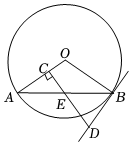如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．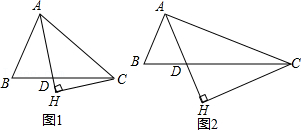
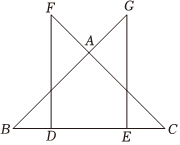如图，在△ABC中，∠B=∠C，在边BC上顺次取点D，E，使BD=CE．作FD⊥BC，GE⊥BC，分别与CA，BA的延长线交于点F，G．求证：GB=FC．
dyczsx2023
2023-07-21
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
如图所示，已知点B，F，C，E在一条直线上，AC=FD，AC∥FD，BF=CE．试说明：AB∥ED．
如图，在△ABC中，D为AB上一点，F为AC上一点，CE∥AB交DF的延长线于点E，若DF=FE，求证：AD=CE．
如图，已知AB=CD，AB∥CD，E、F是AC上两点，且AF=CE，连接BC，求证：∠ABE=∠D．
如图，F、B、E、C四点共线，AB与DE相交于点O，AO=DO，OB=OE，∠A=∠D，求证：EF=BC．
如图，点O是线段AB的中点，OD∥BC且OD=BC，求证：AD=OC．
如图，在△ABC中，AB=AC，D是边BC延长线上的一点，连接AD，过点A，D分别作AE∥BD、DE∥AB，AE、DE交于点E，连接CE．求证：AD=CE．
