服务热线
搜题▪组卷
是某新区的三条规划路，其中AB=6km，AC=3km，∠BAC=60°，
所对的圆心角为60°，新区管委会想在
路边建物资总站点P，在AB，AC路边分别建物资分站点E、F，也就是，分别在
、线段AB和AC上选取点P、E、F．由于总站工作人员每天都要将物资在各物资站点间按P→E→F→P的路径进行运输，因此，要在各物资站点之间规划道路PE、EF和FP．为了快捷、环保和节约成本．要使得线段PE、EF、FP之和最短，试求PE+EF+FP的最小值．（各物资站点与所在道路之间的距离、路宽均忽略不计）
AB=12，
r，
r，
，
，
，
，
﹣3
，
r=3
﹣9
﹣9）km．
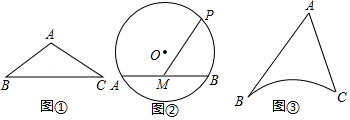
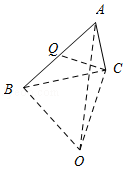
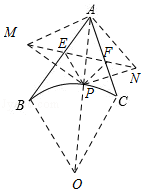
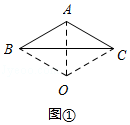
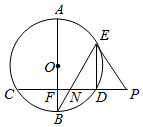如图，已知在⊙O中，直径AB⊥弦CD于点F，P是CD延长线上一点，PE与⊙O相切于点E，连接BE交CD于点N．
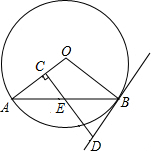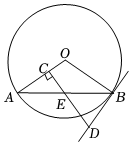如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．
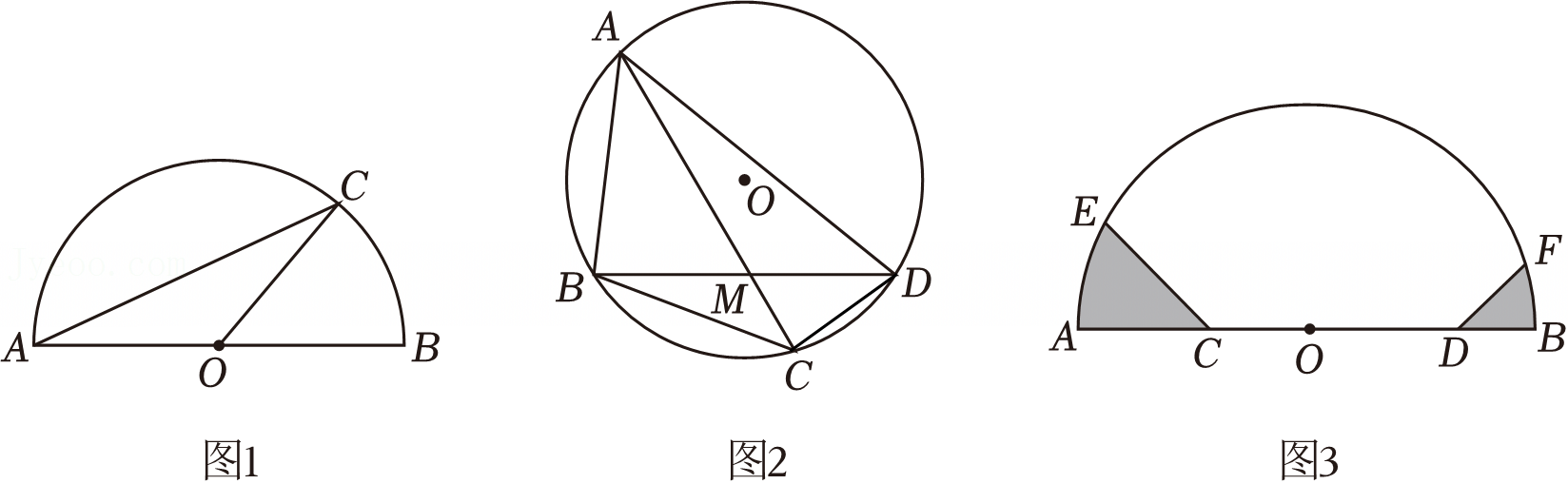
如图，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D．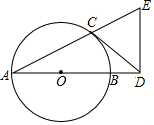
如图，AB是⊙O的直径，点C是⊙O上一点，过点C作⊙O的切线交AB的延长线于点D，过点D作DE⊥AD交AC的延长线于点E．| 甲 | 乙 | |
| 进价（元/件） | 15 | 35 |
| 售价（元/件） | 20 | 45 |
于点E，又测得DE=8m．
，则S△ABC＝ ．
，CD＝2
，是否存在面积最大的四边形？请利用图③说明理由，若存在
上一点，连接AC，CO，则△AOC的最大面积为．
，M为BD上的一点，过点M作一直线AC，AC与BD的夹角成60°，即∠AMB＝60°），与⊙O分别交于A，C两点，求四边形ABCD的最大面积．
所对的圆心角为135°，已知直径AB的长为80cm，记切割掉的图形ACE与图形BDF的面积之和为S，S是否存在最小值？若存在，求出最小值；若不存在，请说明理由．
上一点，BC切半圆O于点B，若AB＝10，BC＝12，则CP的最小值为 ；
米，∠B＝60°，∠BAF＝∠BCD＝150°，DE⊥DC，CD＝20米，劣弧
所对的圆心角为90°，
所在圆的圆心在AF的延长线上，AF＝10米．某天活动课上，九（1）班的同学准备在这块空地上玩游戏，每位同学在游戏开始前，在BC上选取一点P，在弧
上选取一点Q，并在点P和点Q处各插上一面小旗，从点A出发，先到点P处拔下小旗，再到点Q处拔下小旗，用时最短者获胜．已知晓雯和晓静的跑步速度相同，要使用时最短，则所跑的总路程（AP+PQ）应最短，问AP+PQ是否存在最小值？若存在，请你求出AP+PQ的最小值；若不存在，请说明理由．
，动点E、F在AD边上运动，始终保持EF＝3，在BC边上有一个直径为BM的半圆O，连接AM与半圆O交于点N，连接CE、FN，求CE+EF+FN的最小值．
艺黎
2018-07-02
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
如图，M为⊙O内一点，请你利用直尺和圆规作一条弦AB，使得M为AB的中点（不写作法，保留作图痕迹）．
