服务热线
搜题▪组卷
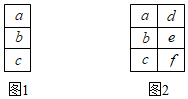 观察下列三行数:
观察下列三行数: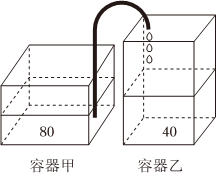 如图,甲、乙两个长方体容器放置在同一水平桌面上,容器甲的底面积为80dm2,高为6dm;容器乙的底面积为40dm2,高为9dm.容器甲中盛满水,容器乙中没有水,现从容器甲向容器乙匀速注水,每分钟注水30dm3.
如图,甲、乙两个长方体容器放置在同一水平桌面上,容器甲的底面积为80dm2,高为6dm;容器乙的底面积为40dm2,高为9dm.容器甲中盛满水,容器乙中没有水,现从容器甲向容器乙匀速注水,每分钟注水30dm3.| A型 | B型 | |
| 价格(万元) | 12 | 10 |
| 处理污水量(吨/月) | 240 | 200 |
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度的部分 | b |
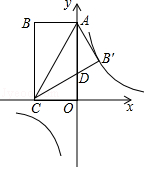
| 第一次 | 第二次 | 第三次 | |
| 手续费/元 | 0 | 1.1 | 0.2 |
word试卷生成中,请等待...