服务热线
搜题▪组卷
某小队在探险过程途中发现一个深坑，小队人员为了测出坑深，采取如下方案：如图所示，在深坑左侧用观测仪AB从观测出发点A观测深坑底部P，且观测视线刚好经过深坑边缘点M，在深坑右侧用观测仪CD从测出发点C观测深坑底部P，且观测视线恰好经过深坑边缘点N，（点E，B，M，N，D，F在同一水平线上）
＝
，
＝
，
，HP＝
，
＝
，
＝
，
＝
＝5.5（m），
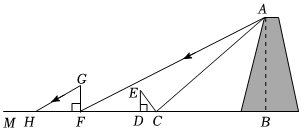小曲和小江为了测量一座宝塔的高度，小曲在小江和宝塔之间的直线BM上的点C处平放一平面镜，在平面镜上做了一个标记，小江看着镜面上的标记，他来回走动，走到点D时，看到宝塔顶端点A在镜面中的像与镜面上的标记重合，这时，测得小江眼睛与地面的高度ED=1.6米，CD=2米，然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小江从D点沿DM方向走了16米，到达宝塔影子的末端F点处，此时，测得小江身高FG的影长FH=3.4米，FG=1.7米．已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出宝塔的高AB的长度．
小明为了测量出一深坑的深度，采取如下方案：如图，在深坑左侧用观测仪AB从观测出发点A观测深坑底部P，且观测视线刚好经过深坑边缘点E，在深坑右侧用观测仪CD从测出发点C观测深坑底部P，且观测视线恰好经过深坑边缘点F，点B，E，F，D在同一水平线上．已知AB⊥EF，CD⊥EF，观测仪AB高2m,观测仪CD高1m,BE=1.6m,FD=0.8m,深坑宽度EF=8.8m,请根据以上数据计算深坑深度多少米？
如图，小华和同伴秋游时，发现在某地小山坡的点E处有一棵小树．他们想利用皮尺、倾角器和平面镜测量小树到山脚下的距离（即DE的长度），小华站在点B处，让同伴移动平面镜至点C处，此时小华在平面镜内可以看到点E．且测得BC=2米，CD=59米，∠CDE=120°．已知小华的身高AB=1.6米，请根据以上数据，求DE的长度．（结果保留根号）
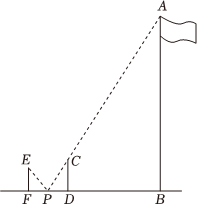
周末，小华和小亮想用所学的数学知识测量家门前小河的宽．测量时，他们选择了河对岸岸边的一棵大树，将其底部作为点A，在他们所在的岸边选择了点B，使得AB与河岸垂直，并在B点竖起标杆BC，再在AB的延长线上选择点D，竖起标杆DE，使得点E与点C、A共线．
5月10日上午，庆祝中国共产主义青年团成立100周年大会在北京人民大会堂隆重举行，习近平总书记重要讲话引发各界青年热烈反响．某校为庆祝共青团成立100周年升起了共青团旗帜，李优和贺基旭想用所学知识测量该旗帜的宽度MN，他们进行了如下操作：如图，首先，李优在C处竖立一根标杆BC，地面上的点A、标杆顶端B和点N在一条直线上，BC=1.5米，AC=1米，AG=8米；然后，贺基旭手持自制直角三角纸板DEF，使长直角边DF与水平地面平行，调整位置，恰好在P点时点D、E、M在一条直线上，DP=1.5米，PG=23.6米，DF=2EF，已知DP⊥PA，MG⊥PA，BC⊥PA，点P、G、C、A在同一水平直线上，点N在MG上，求旗帜的宽度MN．
小明和小亮同学想利用数学知识测量矗立在广场边上的旗杆AB的高度．如图，他们在广场上的D处放置了一根垂直于地面的标杆CD，然后小明笔直地站在F处，小亮在F和D之间找到一个合适的位置P，并在P点处放置了一面小镜子，此时小明恰好看到在镜子里点A和点C重合．已知，点F、P、D、B在同一条直线上，通过测量，BD=8.8m,FD=2.2m,CD=1.8m,小明的眼睛离地面的高度EF=1.5m.求旗杆AB的高度．
如图，小明家窗外有一堵围墙AB，由于围墙的遮挡，清晨太阳光恰好从窗户的最高点C射进房间的地板F处，中午太阳光恰好能从窗户的最低点D射进房间的地板E处，小明测得窗子距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=5m,求围墙AB的高度．
为了测量物体AB的高度，小小带着工具进行测量，方案如下：如图，小小在C处放置一平面镜，她从点C沿BC后退，当退行2米到D处时，恰好在镜子中看到物体顶点A的像，此时测得小小眼睛到地面的距离ED为1.5米；然后，小小在F处竖立了一根高1.8米的标杆FG，发现地面上的点H、标杆顶点G和物体顶点A在一条直线上，此时测得FH为2.6米，DF为3.5米，已知AB⊥BH，ED⊥BH，GF⊥BH，点B、C、D、F、H在一条直线上．请根据以上所测数据，计算AB的高度．
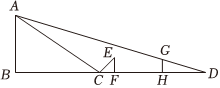小明想用镜子测量一棵松树的高度，如图所示，他把镜子放在点C处（镜子的大小忽略不计），人站在点F时，正好在镜子中看到树顶点A，但由于树旁有一条河，不能直接测量镜子与树之间BC的距离，于是小明从点F向后退到点H处，此时他发现自己的影子和树的影子于地面点D处重合．已知小明身高为1.6米（忽略头顶到眼睛的距离）．经过测量CD=12米，CF=1.8米，DH=3.8米，请你用所学的知识，帮小明求出松树AB的高．
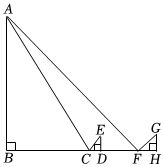一数学兴趣小组为了测量校园内灯柱AB的高度，设计了以下方案：在点C处放一面平面镜，从点C处后退到1m点D处，恰好在平面镜中看到灯柱的顶部A点的像；再将平面镜向后移动4m放在F处（即FC=4m），从点F处向后退1.5m到点H处，恰好再次在平面镜中看到灯柱的顶部A点的像，测得眼睛距地面的高度ED、GH均为1.5m,已知点B，C，D，F，H在同一水平线上，且GH⊥FH，ED⊥CD，AB⊥BH．求灯柱AB的高度．（平面镜的大小忽略不计）
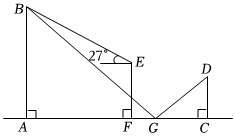周三下午，数学社团的学生在校园进行实践活动，任务是测量校园里玉兰花树AB的高度．小明和小志带着测量工具来到玉兰花树前，小明在空地上选择一点F，把自己的凳子放在F处，站在凳子上测得玉兰花树顶部的仰角为27°，此时小明的眼睛到地面的距离EF=2米．小志走到C处，在自己前方地面的G处放置了一面镜子，恰好能从镜子里看到树的顶端B，此时测得小志的眼睛到地面的距离DC=1.6米．经测量FG=1米，CG=2米，已知点A、F、G、C在同一条直线上，CD⊥AC，EF⊥AC，AB⊥AC，根据以上测量过程及测量数据，请你求出这株玉兰花树AB的高度为多少米．（参考数据：sin27°≈0.45，cos27°≈0.89，tan27°≈0.50）
csyn@dyw.com
2022-06-11
初中数学 | | 解答题
纠错
收藏
下载
相似
组卷
解析
