服务热线
搜题▪组卷
 平面直角坐标系中,直线y=x+6与x轴的负半轴交于点A,与y轴的正半轴交于点B,点C是线段AB的中点,点D在x轴正半轴上,连接CD,将射线CD绕着点C逆时针旋转45°,得到射线CE,射线CE交y轴于点E,连接DE,若△ODE的周长为14,则直线DE的解析式是 .
平面直角坐标系中,直线y=x+6与x轴的负半轴交于点A,与y轴的正半轴交于点B,点C是线段AB的中点,点D在x轴正半轴上,连接CD,将射线CD绕着点C逆时针旋转45°,得到射线CE,射线CE交y轴于点E,连接DE,若△ODE的周长为14,则直线DE的解析式是 .

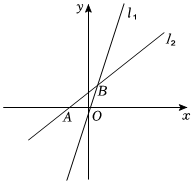 已知直线l2经过点(5,6),交x轴于点A(-3,0),直线l1:y=3x交直线l2于点B.
已知直线l2经过点(5,6),交x轴于点A(-3,0),直线l1:y=3x交直线l2于点B.

 如图,直线y=x+3与x轴交于点A、与y轴交于点B,与经过原点的直线相交于点C(-2,1).
如图,直线y=x+3与x轴交于点A、与y轴交于点B,与经过原点的直线相交于点C(-2,1).


dyczsx2023
2024-03-13
初中数学 | | 解答题