[答案]
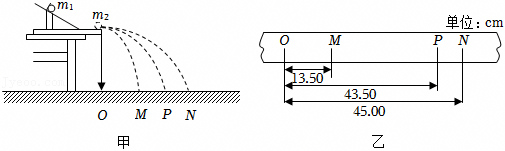
(1)ABD;(2)m1x2=m1x1+m2x3;(3)A;(4)m1x2=﹣m1x1′+m2x3′,由于轨道存在阻力,A小球再次回到水平轨道末端时的速度小于碰撞后的速度,因此x1′偏小,表达式﹣m1x1′+m2x3′偏大,导致A、C小球的末动量大于初动量。
[解析]
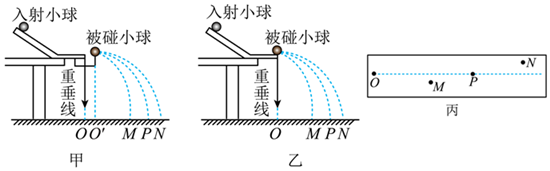
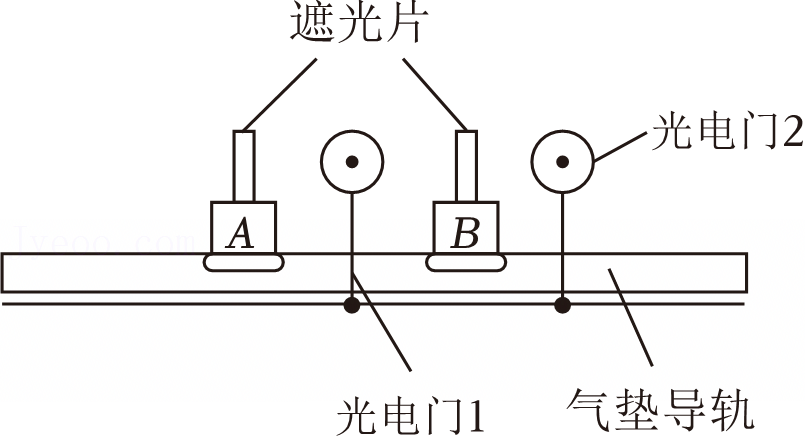
解:(1)为完成本实验,要求知道两球的质量,投影点O到其余三个点的距离,以及能比较准确的找到M、N、P三个点的位置,故还需要的器材是天平、刻度尺和圆规,不需要测时间,故ABD正确,C错误,故选:ABD。
(2)如果系统碰撞动量守恒,设水平向右的方向为正方向,则应该满足
m1v0=m1v1+m2v2
根据两球最终都做平抛运动规律,其平抛运动的时间相等,设为t,有
v0t=x2
v1t=x1
v2t=x3
故上式可变形为m1x2=m1x1+m2x3
(3)实验中能够把速度的测量转化为位移的测量的必要操作保证各个小球均从同一位置被平抛出来,故要求斜槽的末端必须水平,故A正确,BCD错误。故选:A。
(4)由于A球被反向弹回,故动量守恒的表达式变为
m1v0=﹣m1v1+m2v2
同理可变形为
m1x2=﹣m1x1′+m2x3′
由于轨道存在阻力,A小球再次回到水平轨道末端时的速度小于碰撞后的速度,因此x1′偏小,表达式﹣m1x1′+m2x3′偏大,导致A、C小球的末动量大于初动量。
故答案为:(1)ABD;(2)m1x2=m1x1+m2x3;(3)A;(4)m1x2=﹣m1x1′+m2x3′,由于轨道存在阻力,A小球再次回到水平轨道末端时的速度小于碰撞后的速度,因此x1′偏小,表达式﹣m1x1′+m2x3′偏大,导致A、C小球的末动量大于初动量。
[点评]
本题考查了"验证动量守恒定律,",属于"常考题",熟悉题型是解题的关键。
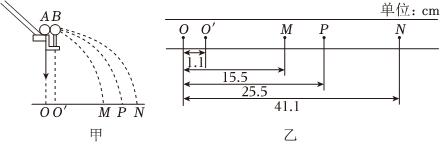
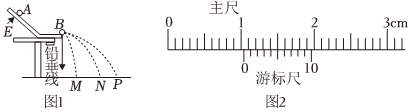
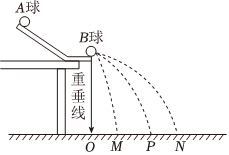 用如图所示的装置验证“动量守恒定律”。实验时先让A球从斜槽上某一固定位置由静止释放,P点为A球落点的平均位置;再把半径相同的B球放在水平轨道末端,将A球仍从原位置由静止释放,M、N分别为A、B两球碰撞后落点的平均位置。O点是水平轨道末端在记录纸上的竖直投影点,O、M、P、N位于同一水平面上。
用如图所示的装置验证“动量守恒定律”。实验时先让A球从斜槽上某一固定位置由静止释放,P点为A球落点的平均位置;再把半径相同的B球放在水平轨道末端,将A球仍从原位置由静止释放,M、N分别为A、B两球碰撞后落点的平均位置。O点是水平轨道末端在记录纸上的竖直投影点,O、M、P、N位于同一水平面上。