服务热线
搜题▪组卷
＝
，
，
AE，
，
×
＝3，
AE+EC＝CE+ET≥CH，
AE+EC≥3，
AE+EC的最小值为3，
PC+PD的最小值为 ．
，连接BD，点E，F分别是边BC，AD上的动点，且BE＝AF，分别过点E，F作EM⊥BD，FN⊥BD，垂足分别为M，N，连接AM，AN，则△AMN周长的最小值为 ．
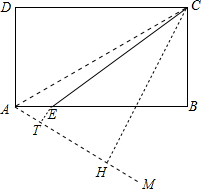
古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所得两长方形面积相等”（如图1“S矩形DNFG=S矩形FEBM”），问题解决：如图2，点P是矩形ABCD的对角线BD上一点，过点P作EF∥BC分别交AB，CD于点E，F，连接AP，CP．若DF=4，EP=3，则图中阴影部分的面积和为 ．
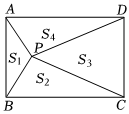如图，P是矩形ABCD内的任意一点，连接PA，PB，PC，PD，得到△PAB，△PBC，△PCD，△PDA，设它们的面积分别是S1，S2，S3，S4．给出以下结论：①S1+S4=S2+S3；②S2+S4=S1+S3；③若S3=2S1，则S4=2S2，其中正确结论的序号是 ．
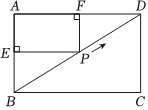如图，矩形ABCD中，AB=6，AD=8，点P从B点沿BD向D点移动，若过点P作AB的垂线交AB于E点，过点P作AD的垂线交AD于F点，则EF的长度最小为 .
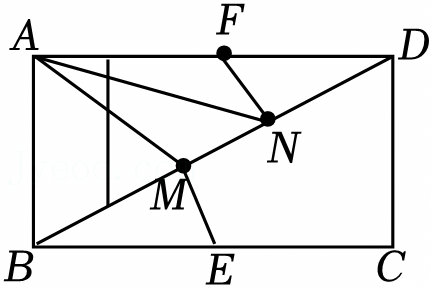
如图，在矩形ABCD中，AB=4，AD=6，点E、F分别在边AB、CD上，点M为线段EF上一动点，过点M作EF的垂线分别交边AD、BC于点G、点H．若线段EF恰好平分矩形ABCD的面积，且DF=1，则GH的长为 ．
tyz511
2019-05-31
初中数学 | | 填空题
纠错
收藏
下载
相似
组卷
解析
如图，在矩形ABCD中，AB=5，BC=6，E、F分别为BC、CD上的动点，且BE=2DF，则DE+2AF的最小值为 ．
如图，以AB为边，在AB的同侧分别作正五边形ABCDE和矩形ABFG，点F，G分别在CD、DE边上，则∠EGA= °．
如图，矩形ABCD的对角线相交于点O作OG⊥AC，交AB于点G，连接CG，若∠BOG=16°，则∠BCG的度数是 ．
如图，矩形ABCD中，AB=2，BC=4，AE为∠BAD的角平分线，F为AE上一动点，M为DF的中点，连接BM，则BM的最小值是 ．
