服务热线
搜题▪组卷
（m），
≈9.8（m），
x2＝﹣1.8，
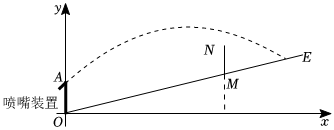
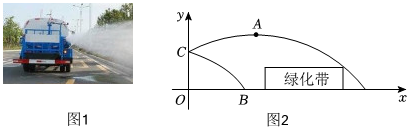
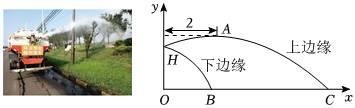如图，灌溉车为绿草地浇水，以点O为坐标原点，OC所在直线为x轴，OH所在直线为y轴，喷水口H离地竖直高度OH为1.2米，可以把灌溉车喷出水的上、下边缘抽象为平面直角坐标系中两条抛物线的部分图象，下边缘抛物线可由上边缘抛物线向左平移得到，上边缘抛物线最高点A离喷水口的水平距离为2米，高出喷水口0.4米．| 制作简易水流装置 | |
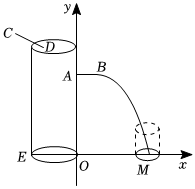
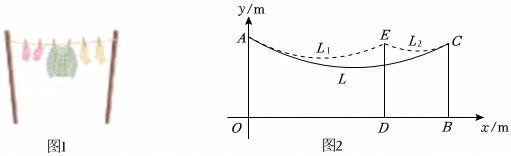
| 设计方案 | 如图，CD是进水通道，AB是出水通道，OE是圆柱形容器的底面直径，从CD将圆柱形容器注满水，内部安装调节器，水流从B处流出且呈抛物线型．以点O为坐标原点，EO所在直线为x轴，OA所在直线为y轴建立平面直角坐标系xOy,水流最终落到x轴上的点M处． |
| 示意图 |
|
| 已知 | AB∥x轴，AB=5cm,OM=15cm,点B为水流抛物线的顶点，点A、B、O、E、M在同一平面内，水流所在抛物线的函数表达式为y=ax2+bx+15（a≠0）． |
| 任务一 | 求水流抛物线的函数表达式； |
| 任务二 | 现有一个底面半径为3cm,高为11cm的圆柱形水杯，将该水杯底面圆的圆心恰好放在M处，水流是否能流到圆柱形水杯内？请通过计算说明理由．（圆柱形水杯的厚度忽略不计） |
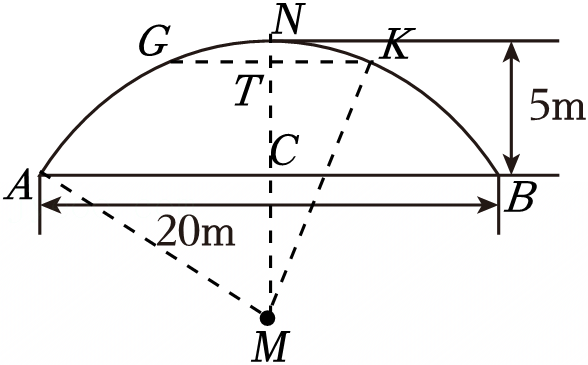
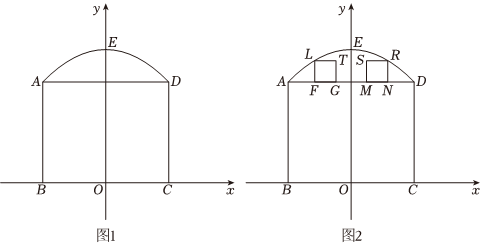
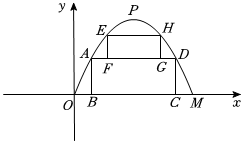白鹿原隧道被称为“中国最大断面黄土隧道”，它的截面近似看作抛物线，某数学课题学习小组，为了研究隧道的截面，建立如图坐标系，已知隧道的净宽OM约为18米，净高（即抛物线最高点到地面的距离）约为12米．在隧道施工过程中，需要一个“凸”字形的支架支撑隧道的顶部，支架的下部分和上部分都分别由矩形ABCD和矩形EFGH组成，已知下部分矩形的长BC=12米，上部分矩形的长宽比（即EH：GH=3：2），点A、D、E、H都在抛物线上．根据以上信息解决问题．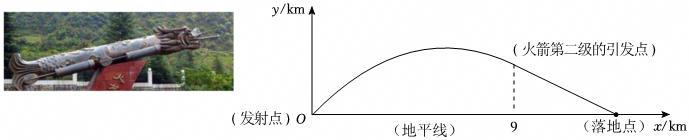
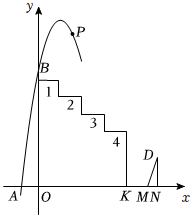．其中，当火箭运行的水平距离为9km时，自动引发火箭的第二级．若火箭第二级的引发点的高度为3.6km．
如图是一个动画设计示意图，x轴上依次有A，O，K、M、N五个点．在OK上方有四个台阶1，2，3，4，每个台阶均平行于x轴，且水平宽度均为2，各个拐角为90°，相邻两个台阶的竖直距离均为2，第1个台阶到x轴距离OB=11．如图，MD为一个可以移动的斜坡，DN⊥x轴，DN=3，MN=1．从点A处向右上方沿抛物线L：y=-x2+4x+12发出一个带光点P．
时，①求h的值；②通过计算判断此球能否过网．
m的Q处时，乙扣球成功，求a的值．
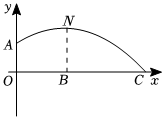这条经过A、N、C三点的抛物线是足球守门员在O处开出一记手抛高球后足球在空中运动到落地的路径图．其中A点离地面1.4米，N点是足球运动过程中的最高点，离地面3.2米，离守门员的水平距离为6米，点C是足球第一次落地的地点．那么足球第一次落地点C距守门员的水平距离为多少米？
）
（a、c为常数，且a≠0）．
word试卷生成中,请等待...
相似
组卷
解析
纠错
收藏
下载
